O sferă este descrisă în jurul unei prisme patrulatere regulate. Prismă dreaptă (quadrangulară regulată)

Tema „Diferite probleme pe poliedre, cilindru, con și bilă” este una dintre cele mai dificile din cursul de geometrie de clasa a XI-a. Înainte de a rezolva probleme geometrice, ei studiază de obicei secțiunile relevante ale teoriei la care se face referire atunci când rezolvă probleme. În manualul lui S. Atanasyan și alții pe această temă (p. 138) se găsesc doar definiții ale unui poliedru descris în jurul unei sfere, ale unui poliedru înscris într-o sferă, ale unei sfere înscrise într-un poliedru și ale unei sfere descrise în jurul unei sfere. poliedru. Recomandările metodologice pentru acest manual (vezi cartea „Studying Geometry in Grades 10–11” de S.M. Sahakyan și V.F. Butuzov, p. 159) spun ce combinații de corpuri sunt luate în considerare la rezolvarea problemelor nr. 629–646 și se atrage atenția. la faptul că „la rezolvarea unei anumite probleme, în primul rând, este necesar să se asigure că elevii au o bună înțelegere a pozițiilor relative ale corpurilor indicate în condiție”. Următoarea este soluția problemelor nr. 638(a) și nr. 640.

Având în vedere toate cele de mai sus, precum și faptul că cele mai dificile probleme pentru elevi sunt combinarea mingii cu alte corpuri, este necesară sistematizarea principiilor teoretice relevante și comunicarea acestora studenților.

Definiții.

1. O minge se numește înscrisă într-un poliedru, iar poliedru descris în jurul unei bile dacă suprafața bilei atinge toate fețele poliedrului.

2. O bilă se numește circumscrisă în jurul unui poliedru, iar poliedru înscris într-o bilă, dacă suprafața bilei trece prin toate vârfurile poliedrului.

3. Se spune că o minge este înscrisă într-un cilindru, trunchi de con (con), iar un cilindru, trunchi de con (con) se spune că este înscris în jurul mingii dacă suprafața mingii atinge bazele (baza) și toate generatoarele cilindrului, trunchi de con (con).

(Din aceasta definitie rezulta ca cercul mare al unei mingi poate fi inscris in orice sectiune axiala a acestor corpuri).

4. Se spune că o minge este circumscrisă unui cilindru, un trunchi de con (con), dacă cercurile bazelor (cercul de bază și vârful) aparțin suprafeței bilei.

(Din aceasta definitie rezulta ca in jurul oricarei sectiuni axiale a acestor corpuri poate fi descris cercul unui cerc mai mare al mingii).

Note generale privind poziția centrului mingii.

1. Centrul unei bile înscrise într-un poliedru se află în punctul de intersecție a planurilor bisectoare ale tuturor unghiurilor diedrice ale poliedrului. Este situat doar în interiorul poliedrului.

2. Centrul unei bile circumscrise unui poliedru se află în punctul de intersecție al planurilor perpendiculare pe toate muchiile poliedrului și care trec prin punctele mijlocii ale acestora. Poate fi amplasat în interiorul, la suprafață sau în exteriorul poliedrului.

Combinație dintre o sferă și o prismă.

1. O bilă înscrisă într-o prismă dreaptă.

Teorema 1. O sferă poate fi înscrisă într-o prismă dreaptă dacă și numai dacă la baza prismei poate fi înscris un cerc, iar înălțimea prismei este egală cu diametrul acestui cerc.

Corolarul 1. Centrul unei sfere înscrise într-o prismă dreaptă se află la mijlocul altitudinii prismei care trece prin centrul cercului înscris în bază.

Corolarul 2. O minge, în special, poate fi înscrisă în linii drepte: triunghiulară, regulată, patruunghiulară (în care sumele laturilor opuse ale bazei sunt egale între ele) cu condiția H = 2r, unde H este înălțimea prismă, r este raza cercului înscris în bază.

2. O sferă circumscrisă unei prisme.

Teorema 2. O sferă poate fi descrisă în jurul unei prisme dacă și numai dacă prisma este dreaptă și un cerc poate fi descris în jurul bazei sale.

Corolarul 1. Centrul unei sfere circumscrise unei prisme drepte se află la mijlocul înălțimii prismei trase prin centrul unui cerc circumscris bazei.

Corolarul 2. O minge, în special, poate fi descrisă: lângă o prismă triunghiulară dreptunghiulară, lângă o prismă regulată, lângă un paralelipiped dreptunghiular, lângă o prismă dreptunghiulară dreptunghiulară, în care suma unghiurilor opuse ale bazei este egală cu 180 de grade.

Din manualul lui L.S. Atanasyan, problemele nr. 632, 633, 634, 637(a), 639(a,b) pot fi sugerate pentru combinarea unei bile și a unei prisme.

Combinația unei mingi cu o piramidă.

1. O minge descrisă lângă o piramidă.

Teorema 3. O minge poate fi descrisă în jurul unei piramide dacă și numai dacă un cerc poate fi descris în jurul bazei sale.

Corolarul 1. Centrul unei sfere circumscrise în jurul unei piramide se află în punctul de intersecție al unei drepte perpendiculare pe baza piramidei care trece prin centrul unui cerc circumscris acestei baze și un plan perpendicular pe orice margine laterală trasată prin mijlocul această margine.

Corolarul 2. Dacă marginile laterale ale piramidei sunt egale între ele (sau înclinate în mod egal față de planul bazei), atunci o minge poate fi descrisă în jurul unei astfel de piramide. Centrul acestei bile se află în acest caz în punctul de intersecție al înălțimea piramidei (sau prelungirea acesteia) cu axa de simetrie a marginii laterale situată în plan marginea laterală și înălțimea.

Corolarul 3. O minge, în special, poate fi descrisă: lângă o piramidă triunghiulară, lângă o piramidă obișnuită, lângă o piramidă patruunghiulară în care suma unghiurilor opuse este de 180 de grade.

2. O minge înscrisă într-o piramidă.

Teorema 4. Dacă fețele laterale ale piramidei sunt înclinate în mod egal față de bază, atunci o minge poate fi înscrisă într-o astfel de piramidă.

Corolarul 1. Centrul unei bile înscrise într-o piramidă ale cărei fețe laterale sunt înclinate egal față de bază se află în punctul de intersecție al înălțimii piramidei cu bisectoarea unghiului liniar al oricărui unghi diedru de la baza piramidei, latura din care este înălțimea feței laterale desenată din vârful piramidei.

Corolarul 2. Puteți încadra o minge într-o piramidă obișnuită.

Din manualul lui L.S. Atanasyan, problemele nr. 635, 637(b), 638, 639(c), 640, 641 pot fi sugerate pentru combinarea unei mingi cu o piramidă.

Combinația unei mingi cu o piramidă trunchiată.

1. O bilă circumscrisă unei piramide trunchiate obișnuite.

Teorema 5. O sferă poate fi descrisă în jurul oricărei piramide trunchiate obișnuite. (Această condiție este suficientă, dar nu necesară)

2. O minge înscrisă într-o piramidă trunchiată obișnuită.

Teorema 6. O bilă poate fi înscrisă într-o piramidă trunchiată obișnuită dacă și numai dacă apotema piramidei este egală cu suma apotemelor bazelor.

Există o singură problemă pentru combinarea unei mingi cu o piramidă trunchiată în manualul lui L.S. Atanasyan (nr. 636).

Combinație de minge cu corpuri rotunde.

Teorema 7. O sferă poate fi descrisă în jurul unui cilindru, a unui trunchi de con (circular drept) sau a unui con.

Teorema 8. O bilă poate fi înscrisă într-un cilindru (circular drept) dacă și numai dacă cilindrul este echilateral.

Teorema 9. Puteți introduce o minge în orice con (circular drept).

Teorema 10. O bilă poate fi înscrisă într-un trunchi de con (circular drept) dacă și numai dacă generatorul ei este egal cu suma razelor bazelor.

Din manualul lui L.S. Atanasyan, problemele nr. 642, 643, 644, 645, 646 pot fi sugerate pentru combinarea unei mingi cu corpuri rotunde.

Pentru a studia cu mai mult succes materialul pe această temă, este necesar să includeți sarcini orale în lecții:

1. Muchia cubului este egală cu a. Aflați razele bilelor: înscrise în cub și circumscrise în jurul acestuia. (r = a/2, R = a3).

2. Se poate descrie o sferă (minge) în jurul: a) unui cub; b) paralelipiped dreptunghiular; c) un paralelipiped înclinat cu un dreptunghi la bază; d) paralelipiped drept; e) un paralelipiped înclinat? (a) da; b) da; c) nu; d) nu; d) nu)

3. Este adevărat că o sferă poate fi descrisă în jurul oricărei piramide triunghiulare? (Da)

4. Este posibil să descriem o sferă în jurul oricărei piramide patrulatere? (Nu, nu aproape de nicio piramidă patruunghiulară)

5. Ce proprietăți trebuie să aibă o piramidă pentru a descrie o sferă din jurul ei? (La baza sa ar trebui să existe un poligon în jurul căruia poate fi descris un cerc)

6. Într-o sferă este înscrisă o piramidă, a cărei margine laterală este perpendiculară pe bază. Cum să găsești centrul unei sfere? (Centrul sferei este punctul de intersecție a două locuri geometrice de puncte din spațiu. Primul este o perpendiculară trasată pe planul bazei piramidei, prin centrul unui cerc circumscris în jurul acesteia. Al doilea este un plan perpendicular pe o margine laterală dată și tras prin mijlocul ei)

7. În ce condiții poți descrie o sferă în jurul unei prisme, la baza căreia se află un trapez? (În primul rând, prisma trebuie să fie dreaptă, iar în al doilea rând, trapezul trebuie să fie isoscel, astfel încât să poată fi descris un cerc în jurul său)

8. Ce condiții trebuie să îndeplinească o prismă pentru ca o sferă să fie descrisă în jurul ei? (Prisma trebuie să fie dreaptă, iar baza sa trebuie să fie un poligon în jurul căruia poate fi descris un cerc)

9. O sferă este descrisă în jurul unei prisme triunghiulare, al cărei centru se află în afara prismei. Care triunghi este baza prismei? (triunghi obtuz)

10. Este posibil să descriem o sferă în jurul unei prisme înclinate? (Nu, nu poti)

11. În ce condiție va fi situat centrul unei sfere circumscrise unei prisme triunghiulare dreptunghiulare pe una dintre fețele laterale ale prismei? (Baza este un triunghi dreptunghic)

12. Baza piramidei este un trapez isoscel.Proiecția ortogonală a vârfului piramidei pe planul bazei este un punct situat în afara trapezului. Este posibil să descrii o sferă în jurul unui astfel de trapez? (Da, poți. Faptul că proiecția ortogonală a vârfului piramidei este situată în afara bazei acesteia, nu contează. Este important ca la baza piramidei să se afle un trapez isoscel - un poligon în jurul căruia poate fi un cerc. descris)

13. O sferă este descrisă lângă o piramidă obișnuită. Cum este situat centrul său în raport cu elementele piramidei? (Centrul sferei se află pe o perpendiculară trasă pe planul bazei prin centrul acesteia)

14. În ce stare se află centrul unei sfere descrise în jurul unei prisme triunghiulare dreptunghiulare: a) în interiorul prismei; b) în afara prismei? (La baza prismei: a) un triunghi ascuțit; b) triunghi obtuz)

15. O sferă este descrisă în jurul unui paralelipiped dreptunghiular ale cărui margini sunt de 1 dm, 2 dm și 2 dm. Calculați raza sferei. (1,5 dm)

16. În ce trunchi de con se poate încadra o sferă? (Într-un trunchi de con, în a cărui secțiune axială poate fi înscris un cerc. Secțiunea axială a conului este un trapez isoscel, suma bazelor sale trebuie să fie egală cu suma laturilor sale laterale. Cu alte cuvinte, suma razelor bazelor conului trebuie să fie egală cu generatorul)

17. O sferă este înscrisă într-un trunchi de con. În ce unghi este vizibilă generatria conului din centrul sferei? (90 de grade)

18. Ce proprietate trebuie să aibă o prismă dreaptă pentru ca o sferă să fie înscrisă în ea? (În primul rând, la baza unei prisme drepte trebuie să existe un poligon în care să poată fi înscris un cerc și, în al doilea rând, înălțimea prismei trebuie să fie egală cu diametrul cercului înscris în bază)

19. Dați un exemplu de piramidă care nu poate încăpea o sferă? (De exemplu, o piramidă patruunghiulară cu un dreptunghi sau un paralelogram la bază)

20. La baza unei prisme drepte se află un romb. Este posibil să potriviți o sferă în această prismă? (Nu, este imposibil, deoarece, în general, este imposibil să descrii un cerc în jurul unui romb)

21. În ce condiție poate fi înscrisă o sferă într-o prismă triunghiulară dreptunghiulară? (Dacă înălțimea prismei este de două ori mai mare decât raza cercului înscris în bază)

22. În ce condiție poate fi înscrisă o sferă într-o piramidă trunchiată patruunghiulară obișnuită? (Dacă secțiunea transversală a unei piramide date este un plan care trece prin mijlocul laturii bazei perpendicular pe aceasta, este un trapez isoscel în care poate fi înscris un cerc)

23. O sferă este înscrisă într-o piramidă trunchiată triunghiulară. Care punct al piramidei este centrul sferei? (Centrul sferei înscrise în această piramidă se află la intersecția a trei planuri bisectrale de unghiuri formate de fețele laterale ale piramidei cu baza)

24. Este posibil să descrii o sferă în jurul unui cilindru (circular dreapta)? (Da, poti)

25. Este posibil să descriem o sferă în jurul unui con, un trunchi de con (circular drept)? (Da, poți, în ambele cazuri)

26. Poate fi înscrisă o sferă în orice cilindru? Ce proprietăți trebuie să aibă un cilindru pentru a potrivi o sferă în el? (Nu, nu de fiecare dată: secțiunea axială a cilindrului trebuie să fie pătrată)

27. Poate fi înscrisă o sferă în orice con? Cum se determină poziția centrului unei sfere înscrise într-un con? (Da, absolut. Centrul sferei înscrise se află la intersecția altitudinii conului și bisectoarea unghiului de înclinare a generatricei față de planul bazei)

Autorul consideră că din cele trei lecții de planificare pe tema „Diferite probleme pe poliedre, cilindru, con și minge”, este indicat să se dedice două lecții rezolvării problemelor legate de combinarea unei mingi cu alte corpuri. Nu se recomandă demonstrarea teoremelor date mai sus din cauza timpului insuficient la clasă. Puteți invita studenții care au abilități suficiente pentru acest lucru să le demonstreze, indicând (la discreția profesorului) cursul sau planul probei.

În jurul unei sfere este descrisă o prismă patruunghiulară regulată, al cărei volum este de 65 dm 3. Calculați raportul dintre suprafața totală a prismei și volumul sferei
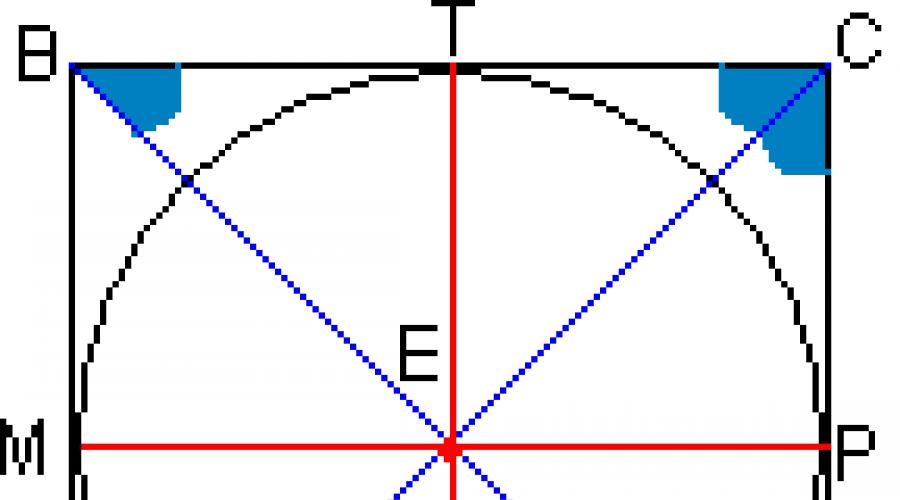
O prismă se numește regulată dacă bazele sale sunt poligoane regulate și marginile sale laterale sunt perpendiculare pe bază. Un patrulater regulat este un pătrat. Punctul de intersecție al diagonalelor unui pătrat este centrul acestuia, precum și centrul cercului înscris în el. Să demonstrăm acest fapt. deși această dovadă este puțin probabil să fie cerută și poate fi omisă
Ca tip special de paralelogram, dreptunghi și romb, pătratul are proprietățile lor: diagonalele sunt egale și bisectate de punctul de intersecție și sunt bisectoare ale colțurilor pătratului. Prin punctul E trasăm o dreaptă TK paralelă cu AB. AB este perpendicular pe BC, ceea ce înseamnă că TC este, de asemenea, perpendicular pe BC (dacă una dintre cele două drepte paralele este perpendiculară pe oricare a treia dreaptă, atunci a doua linie paralelă este perpendiculară pe această (a treia) dreaptă). În același mod vom efectua direct MR. Triunghiurile dreptunghiulare BET și AEK sunt egale ca ipotenuză și unghi ascuțit (BE=AE - jumătate din diagonale, ∠ EBT=∠ EAK - jumătate din unghiul drept), ceea ce înseamnă ET=EK. În același mod demonstrăm că EM=EP. Și din egalitatea triunghiurilor CEP și CET (același semn) vedem că ET = EP, adică. ET=EP=EK=EM sau pur și simplu spuneți că punctul M este echidistant de laturile pătratului, iar aceasta este o condiție necesară pentru a-l recunoaște ca centru al unui cerc înscris în acest pătrat.
Luați în considerare dreptunghiul AVTC (acest patrulater este un dreptunghi, deoarece toate unghiurile din el sunt unghiuri drepte prin construcție). Într-un dreptunghi, laturile opuse sunt egale - AB = CT (trebuie remarcat că CT este diametrul bazei) - aceasta înseamnă că latura bazei este egală cu diametrul cercului înscris.
Să desenăm plane prin paralel (două drepte perpendiculare pe același plan sunt paralele) AA 1, CC 1 și BB 1 și respectiv DD 1 (liniile paralele definesc un singur plan). Planurile AA 1 C 1 C și BB 1 D 1 D sunt perpendiculare pe baza ABCD, deoarece trec prin linii drepte (nerve laterale) perpendiculare pe acesta.
Din punctul H (intersecția diagonalelor) în planul AA 1 C 1 C perpendicular pe baza ABCD. Atunci vom proceda la fel și în planul BB 1 D 1 D. Din teoremă: dacă dintr-un punct aparținând unuia dintre cele două plane perpendiculare trasăm o perpendiculară pe celălalt plan, atunci această perpendiculară se află complet în primul plan, vom găsiți că această perpendiculară trebuie să se afle și în planul AA 1 C 1 C și în planul BB 1 D 1 D. Acest lucru este posibil numai dacă această perpendiculară coincide cu linia de intersecție a acestor plane - NU. Acestea. segmentul NU este o linie dreaptă pe care se află centrul cercului înscris (întrucât NU este echidistant de planurile fețelor laterale, iar aceasta decurge la rândul său din echidistanța punctelor E și H față de vârfurile bazelor corespunzătoare). (după ceea ce s-a dovedit: punctul de intersecție al diagonalelor este echidistant de laturile pătratului ), iar din faptul că NOT este perpendicular pe baze, putem concluziona că NOT este diametrul bilei. Teorema . O bilă poate fi înscrisă într-o prismă regulată dacă și numai dacă înălțimea ei este egală cu diametrul cercului înscris în bază. Ei bine, este deja înscrisă în prisma noastră, ceea ce înseamnă că înălțimea ei este egală cu diametrul lui cercul înscris în bază.Dacă desemnăm latura bazei ca A, iar înălțimea prismei este h, atunci folosind această teoremă concluzionăm A=h și atunci volumul prismei se găsește astfel:

Apoi, folosind faptul că înălțimea este egală cu diametrul bilei înscrise și cu latura bazei prismei, găsim raza bilei și apoi volumul acesteia:

Trebuie spus că marginile laterale sunt egale cu înălțimea (segmentele de linii paralele închise între plane paralele sunt egale), iar deoarece înălțimea este egală cu latura bazei, atunci în general toate marginile prismei sunt egale. unul față de celălalt, iar toate fețele sunt în esență pătrate cu arie A 2. De fapt, o astfel de figură se numește cub - un caz special de paralelipiped. Rămâne să găsiți suprafața totală a cubului și să o raportați la volumul mingii:

2. Partea bazei

Sarcini

1. Aflați aria suprafeței unei prisme drepte, la baza căreia se află un romb cu diagonalele egale cu 3 și 4 și o margine laterală egală cu 5.

Raspuns: 62.

2. La baza unei prisme drepte se află un romb cu diagonalele egale cu 6 și 8. Suprafața sa este de 248. Aflați marginea laterală a acestei prisme.

Raspuns: 10.

3. Aflați marginea laterală a unei prisme pătraunghiulare regulate dacă laturile bazei sale sunt 3 și aria suprafeței este 66.

Raspuns: 4.

4. O prismă patruunghiulară obișnuită este circumscrisă unui cilindru a cărui rază de bază și înălțime sunt egale cu 2. Aflați aria suprafeței laterale a prismei.

Raspuns: 32.

5. O prismă patruunghiulară obișnuită este circumscrisă unui cilindru a cărui rază de bază este 2. Aria suprafeței laterale a prismei este de 48. Aflați înălțimea cilindrului.

Prismă dreaptă (hexagonală regulată)

O prismă în care marginile laterale sunt perpendiculare pe baze, iar bazele sunt pătrate egale.

1. Fețe laterale - dreptunghiuri egale

2. Partea bazei

Sarcini

1. Aflați volumul unei prisme hexagonale regulate ale cărei laturi de bază sunt egale cu 1 și ale cărei margini laterale sunt egale cu .

Răspuns: 4.5.

2. Aflați aria suprafeței laterale a unei prisme hexagonale regulate ale cărei laturi de bază sunt 3 și a cărei înălțime este 6.

Raspuns: 108.

3. Aflați volumul unei prisme hexagonale regulate, ale cărei margini sunt egale cu √3.

Răspuns: 13.5

4. Aflați volumul poliedrului ale cărui vârfuri sunt punctele A, B, C, D, A1, B1, C1, D1 ale unei prisme hexagonale regulate ABCDEFA1B1C1D1E1F1, a cărei aria bazei este 6 și marginea laterală este 2.

Prismă dreaptă (arbitrară n-cărbune)

O prismă ale cărei margini laterale sunt perpendiculare pe baze, iar bazele sunt n-goni egale.

1. Dacă baza este un poligon regulat, atunci fețele laterale sunt dreptunghiuri egale.

2. Partea bazei .

Piramidă

O piramidă este un poliedru compus dintr-un n-gon A1A2...AnA1 și n triunghiuri (A1A2P, A1A3P etc.).

1. Secțiunea paralelă cu baza piramidei este un poligon asemănător bazei. Zonele secțiunii transversale și zonele de bază sunt legate ca pătratele distanțelor lor până la vârful piramidei.

2. O piramidă se numește regulată dacă baza ei este un poligon regulat și vârful ei este proiectat în centrul bazei.

3. Toate muchiile laterale ale unei piramide regulate sunt egale, iar fețele laterale sunt triunghiuri isoscele egale.

4. Înălțimea feței laterale a unei piramide obișnuite se numește apotema.

5. Aria suprafeței laterale a unei piramide regulate este egală cu jumătate din produsul dintre perimetrul bazei și apotema.

Sarcini

1. De câte ori va crește volumul unui tetraedru obișnuit dacă toate marginile sale sunt dublate?

Raspuns: 8.

2. Laturile bazei unei piramide hexagonale regulate sunt egale cu 10, marginile laterale sunt egale cu 13. Aflați aria suprafeței laterale a piramidei.

Raspuns: 360.

5. Aflați volumul piramidei prezentate în figură. Baza sa este un poligon, ale cărui laturi adiacente sunt perpendiculare, iar una dintre marginile laterale este perpendiculară pe planul bazei și egală cu 3.

Raspuns: 27.

6. Aflați volumul unei piramide triunghiulare regulate ale cărei laturi de bază sunt egale cu 1 și a cărei înălțime este egală cu .

Răspuns: 0,25.

7. Marginile laterale ale unei piramide triunghiulare sunt reciproc perpendiculare, fiecare dintre ele fiind egală cu 3. Aflați volumul piramidei.

Răspuns: 4.5.

8. Diagonala bazei unei piramide patrulatere regulate este 8. Muchia laterală este 5. Aflați volumul piramidei.

Raspuns: 32.

9. Într-o piramidă patruunghiulară obișnuită, înălțimea este 12 și volumul este 200. Aflați marginea laterală a piramidei.

Raspuns: 13.

10. Laturile bazei unei piramide patruunghiulare obișnuite sunt egale cu 6, marginile laterale sunt egale cu 5. Aflați aria suprafeței piramidei.

Raspuns: 84.

11. Volumul unei piramide hexagonale regulate este 6. Latura bazei este 1. Aflați muchia laterală.

12. De câte ori va crește aria suprafeței unui tetraedru obișnuit dacă toate marginile sale sunt dublate?

Raspuns: 4.

13. Volumul unei piramide patruunghiulare obișnuite este 12. Aflați volumul piramidei tăiat de ea de un plan care trece prin diagonala bazei și mijlocul muchiei laterale opuse.

Raspuns: 3.

14. De câte ori va scădea volumul octaedrului dacă toate muchiile lui sunt înjumătățite?

Raspuns: 8.

15. Volumul unei piramide triunghiulare este 15. Planul trece prin latura bazei acestei piramide și intersectează marginea laterală opusă într-un punct care o împarte în raport de 1: 2, numărând din vârful piramidei. Găsiți cel mai mare volum al piramidelor în care planul împarte piramida originală.

Raspuns: 10.

16. Aflați înălțimea unei piramide triunghiulare regulate ale cărei laturi de bază sunt egale cu 2 și al cărei volum este egal cu .

Raspuns: 3.

17. Într-o piramidă patruunghiulară obișnuită, înălțimea este 6, marginea laterală este 10. Aflați volumul acesteia.

Răspuns: 256.

18. Dintr-o piramidă triunghiulară, al cărei volum este 12, o piramidă triunghiulară este tăiată de un plan care trece prin vârful piramidei și linia mediană a bazei. Aflați volumul piramidei triunghiulare tăiate.

Raspuns: 3.

Cilindru

Un cilindru este un corp delimitat de o suprafață cilindrică și două cercuri cu limite.

H

R

Volumul corpului	Suprafața laterală	Zona de bază	Suprafata totala

1. Generatoare ale unui cilindru - segmente de generatoare închise între baze.

2. Înălțimea cilindrului este lungimea generatricei.

3. Secțiunea axială este un dreptunghi, dintre care două laturi sunt generatrice, iar celelalte două sunt diametrele bazelor cilindrului.

4. Secțiune circulară - secțiune al cărei plan de tăiere este perpendicular pe axa cilindrului.

5. Dezvoltarea suprafeței laterale a cilindrului - un dreptunghi reprezentând două margini ale tăieturii suprafeței laterale a cilindrului de-a lungul generatricei.

6. Zona suprafeței laterale a cilindrului este zona de dezvoltare a acestuia.

7. Suprafața totală a unui cilindru se numește suma ariilor suprafeței laterale și a celor două baze.

8. Puteți descrie oricând o sferă în jurul unui cilindru. Centrul său se află la mijlocul înălțimii. , unde R este raza bilei, r este raza bazei cilindrului, H este înălțimea cilindrului.

9. Puteți introduce o minge într-un cilindru dacă diametrul bazei cilindrului este egal cu înălțimea acestuia, .

Sarcini

1. O parte este coborâtă într-un vas cilindric care conține 6 litri de apă. În același timp, nivelul lichidului din vas a crescut de 1,5 ori. Care este volumul piesei?

Raspuns: 3.

2. Găsiți volumul unui cilindru a cărui aria bazei este 1, generatoarea sa este 6 și este înclinată față de planul bazei la un unghi de 30°.

Raspuns: 3.

3. Cilindrul și conul au o bază și o înălțime comune. Aflați volumul cilindrului dacă volumul conului este 50.

Raspuns: 150.

4. Apa, situată într-un vas cilindric la nivelul de 12 cm, a fost turnată într-un vas cilindric de două ori mai mare în diametru. La ce înălțime va fi nivelul apei în al doilea vas?

5. Aria secțiunii transversale axiale a cilindrului este egală cu . Găsiți aria suprafeței laterale a cilindrului.

Raspuns: 2.

6. O prismă patruunghiulară obișnuită este circumscrisă unui cilindru a cărui rază de bază și înălțime sunt egale cu 2. Aflați aria suprafeței laterale a prismei.

Raspuns: 32.

7. Circumferința bazei cilindrului este 3. Aria suprafeței laterale este 6. Aflați înălțimea cilindrului.

8. O cană cilindrică este de două ori mai înaltă decât a doua, dar a doua este de o ori și jumătate mai lată. Găsiți raportul dintre volumul celei de-a doua căni și volumul primei.

Răspuns: 1.125.

9. Intr-un vas cilindric nivelul lichidului ajunge la 18 cm.La ce inaltime va fi nivelul lichidului daca este turnat intr-un al doilea vas al carui diametru este de 3 ori mai mare decat primul?

Raspuns: 2.

Con

Un con este un corp delimitat de o suprafață conică și un cerc.

axa conului

R

vârf

formare

suprafata laterala

r

Volumul corpului	Suprafața laterală	Zona de bază	Suprafata totala

1. Zona suprafeței laterale a conului este zona de dezvoltare a acestuia.

2. Relația dintre unghiul de măturare și unghiul de vârf al secțiunii axiale .

1. Un cilindru și un con au o bază și o înălțime comune. Aflați volumul cilindrului dacă volumul conului este 50.

Raspuns: 150.

2. Aflați volumul unui con a cărui suprafață a bazei este 2, generatoarea sa este 6 și este înclinată față de planul bazei la un unghi de 30°.

Raspuns: 2.

3. Volumul conului este de 12. Se trasează o secțiune paralelă cu baza conului, împărțind înălțimea la jumătate. Găsiți volumul conului tăiat.

Răspuns: 1.5.

4. De câte ori este volumul unui con circumscris unei piramide patruunghiulare obișnuite mai mare decât volumul unui con înscris în această piramidă?

Raspuns: 2.

5. Înălțimea conului este 6, generatoarea este 10. Aflați volumul împărțit la .

Raspuns: 128.

6. Cilindrul și conul au o bază și o înălțime comune. Aflați volumul conului dacă volumul cilindrului este 48.

Raspuns: 16.

7. Diametrul bazei conului este de 6, iar unghiul la vârful secțiunii axiale este de 90°. Calculați volumul conului împărțit la .

8. Un con este descris în jurul unei piramide patruunghiulare regulate cu o latură de bază de 4 și o înălțime de 6. Aflați volumul împărțit la .

9. Un con se obține prin rotirea unui triunghi dreptunghic isoscel în jurul unui catet egal cu 6. Aflați volumul împărțit la .

Sferă și minge

O sferă este o suprafață formată din toate punctele din spațiu situate la o distanță dată de un punct dat. O minge este un corp delimitat de o sferă.

1. O secțiune a unei sfere de către un plan este un cerc dacă distanța de la centrul sferei la plan este mai mică decât raza sferei.

2. Secțiunea unei mingi de către un plan este un cerc.

3. Un plan tangent la o sferă este un plan care are un singur punct comun cu sfera.

4. Raza sferei, trasă la punctul de contact al sferei cu planul, este perpendiculară pe planul tangent.

5. Dacă raza unei sfere este perpendiculară pe planul care trece prin capătul său situat pe sferă, atunci acest plan este tangent la sferă.

6. Se spune că un poliedru este circumscris unei sfere dacă sfera atinge toate fețele sale.

7. Segmentele de tangente la o sferă trase dintr-un punct sunt egale și formează unghiuri egale cu o dreaptă care trece prin acest punct și centrul sferei.

8. O sferă este înscrisă într-o suprafață cilindrică dacă atinge toți generatorii ei.

9. O sferă este înscrisă într-o suprafață conică dacă atinge toți generatorii ei.

Sarcini

1. Razele a două bile sunt 6 și 8. Aflați raza unei bile a cărei suprafață este egală cu suma suprafețelor lor.

Raspuns: 10.

2. Aria cercului mare al mingii este 1. Aflați aria suprafeței mingii.

3. De câte ori va crește suprafața mingii dacă raza ei este dublată?

4. Razele a trei bile sunt 3, 4 și 5. Aflați raza unei bile al cărei volum este egal cu suma volumelor lor.

Raspuns: 6.

5. Un paralelipiped dreptunghiular este descris în jurul unei sfere cu raza 2. Găsiți-i aria suprafeței.

Raspuns: 96.

6. Un cub este înscris într-o bilă de rază . Găsiți aria suprafeței cubului.

Raspuns: 24.

7. Un paralelipiped dreptunghiular este descris în jurul unei sfere cu raza 2. Aflați-i volumul.

8. Volumul unui paralelipiped dreptunghiular circumscris unei sfere este de 216. Aflați raza sferei.

Raspuns: 3.

9. Aria suprafeței unui paralelipiped dreptunghiular circumscris în jurul unei sfere este de 96. Aflați raza sferei.

Raspuns: 2.

10. În jurul mingii este descris un cilindru, a cărui suprafață laterală este de 9. Găsiți suprafața mingii.

Raspuns: 9.

11. De câte ori este aria suprafeței unei sfere circumscrise unui cub mai mare decât aria unei sfere înscrise în același cub?

Raspuns: 3.

12. Un cub este înscris într-o bilă de rază . Aflați volumul cubului.

Raspuns: 8.

Poliedre compozite

Sarcini

1. Figura prezintă un poliedru, toate unghiurile diedrice ale poliedrului sunt unghiuri drepte. Aflați distanța dintre vârfurile A și C2.

Raspuns: 3.

2. Aflați unghiul CAD2 al poliedrului prezentat în figură. Toate unghiurile diedrice ale unui poliedru sunt unghiuri drepte. Dați răspunsul în grade.

Raspuns: 60.

3. Găsiți aria suprafeței poliedrului prezentat în figură (toate unghiurile diedrice sunt unghiuri drepte).

Raspuns: 18.

4. Găsiți aria suprafeței poliedrului prezentat în figură (toate unghiurile diedrice sunt unghiuri drepte).

Raspuns: 132

5. Găsiți aria suprafeței crucii spațiale prezentate în figură și compusă din cuburi de unitate.

Raspuns: 30

6. Aflați volumul poliedrului prezentat în figură (toate unghiurile diedrice sunt drepte).

Răspuns: 8

7.Aflați volumul poliedrului prezentat în figură (toate unghiurile diedrice sunt drepte).

Raspuns: 78

8. Figura prezintă un poliedru, toate unghiurile diedrice ale poliedrului sunt unghiuri drepte. Aflați tangenta unghiului ABB3.

Raspuns: 2

10. Figura prezintă un poliedru, toate unghiurile diedrice ale poliedrului sunt unghiuri drepte. Aflați tangenta unghiului C3D3B3.

Raspuns: 3

11. Prin linia de mijloc a bazei prismei triunghiulare se trasează un plan paralel cu marginea laterală. Găsiți aria suprafeței laterale a prismei dacă aria suprafeței laterale a prismei triunghiulare tăiate este 37.

Raspuns: 74.

12. Figura prezintă un poliedru, toate unghiurile diedrice ale poliedrului sunt unghiuri drepte. Aflați pătratul distanței dintre vârfurile B2 și D3.

Raspuns: 11.

O minge poate fi descrisă în jurul unei piramide dacă și numai dacă un cerc poate fi descris în jurul bazei sale.

Pentru a construi centrul O al acestei mingi, aveți nevoie de:

1. Aflați centrul O al cercului circumscris bazei.

2. Prin punctul O, trasați o dreaptă perpendiculară pe planul bazei.

3. Desenați un plan prin mijlocul oricărei margini laterale a piramidei perpendicular pe această muchie.

4. Aflați punctul O al intersecției dreptei și planului construit.

Caz special: marginile laterale ale piramidei sunt egale. Apoi:

mingea poate fi descrisă;

centrul O al mingii se află la înălțimea piramidei;

Unde este raza sferei circumscrise; - coasta laterala; H este înălțimea piramidei.

5.2. Bilă și prismă

O sferă poate fi descrisă în jurul unei prisme dacă și numai dacă prisma este dreaptă și un cerc poate fi descris în jurul bazei sale.

Centrul mingii este mijlocul segmentului care leagă centrele cercurilor descrise lângă baze.

unde este raza sferei circumscrise; - raza cercului descris lângă bază; H este înălțimea prismei.

5.3. Bilă și cilindru

O minge poate fi întotdeauna descrisă în jurul unui cilindru. Centrul bilei este centrul de simetrie al secțiunii axiale a cilindrului.

5.4. Minge și con

O minge poate fi întotdeauna descrisă în jurul unui con. Centrul mingii; servește ca centru al unui cerc circumscris secțiunii axiale a conului.

Pentru a utiliza previzualizările prezentării, creați un cont Google și conectați-vă la el: https://accounts.google.com

Subtitrările diapozitivelor:

Sfere descrise în jurul poliedrelor.

Definiție. Se spune că un poliedru este înscris într-o sferă (și o sferă descrisă despre un poliedru) dacă toate vârfurile poliedrului aparțin acestei sfere. Consecinţă. Centrul sferei circumscrise este un punct echidistant de toate vârfurile poliedrului. O O O . . .

Teorema 1. Mulțimea punctelor echidistante de două puncte date este un plan perpendicular pe un segment cu capete în puncte date, care trece prin mijlocul acestuia (planul bisectoarelor perpendiculare pe acest segment). AB ┴ α AO=OB α A B O

Teorema 2. Mulțimea punctelor echidistante de n puncte date situate pe același cerc este o dreaptă perpendiculară pe planul acestor puncte, care trece prin centrul cercului circumscris lor. C E A B D O a . . . . . . C E A B D . . . . .

O prismă înscrisă într-o sferă. OA=OB=…=OX=R sf. O 1. O. O sf a 1 a .A 1 .B 1 .C 1 .D 1 E 1 . X 1. .A .B .C .D E. X. a a 1 . O. O 1

Consecințe. 1) O sferă poate fi descrisă în jurul unei prisme triunghiulare drepte, deoarece Puteți descrie oricând un cerc în jurul unui triunghi. 2) O sferă poate fi descrisă în jurul oricărei prisme regulate, deoarece o prismă regulată este dreaptă și un cerc poate fi întotdeauna descris în jurul unui poliedru regulat. O. O. .

Sarcina nr. 1. Bila este circumscrisă în jurul unei prisme, la baza căreia se află un triunghi dreptunghic cu catetele 6 și 8. Marginea laterală a prismei este 24. Aflați Raza bilei. Dat: ∆ ABC – dreptunghiular; AC=6, BC=8, AA1 =24. Găsiți: Rw = ? Rezolvare: 1)OO 1 ┴AB 1 ; OO 1 =AA 1 =24. 2) ABC: AB=10. 3) O w OB: R w = O w B=√OO w 2 + OB 2 = = √144+25=13 Răspuns: 13. O 1 O. . . R w Osh C 1 B 1 A 1 A C B

Sarcina nr. 3. Dimensiunile unui cuboid sunt 2,3 și 5. Aflați raza sferei circumscrise. Dat:AB=a=2; BC=b=3; CC 1 =c=5. Găsiți: Rw = ? Rezolvare: 1) AC 2 =a 2 +b 2 +c 2. 2) A 1 C 2 =25+9+4=38 (Proprietatea diagonalelor unui paralelipiped dreptunghic) 3) A 1 C=√38; R w = O w C = √38 /2 Răspuns: √38 /2 D 1 C 1 B 1 A 1 A B C D 5 2 3 . . . O sh

Sarcina nr. 3. Latura bazei unei prisme triunghiulare regulate este egală cu a, iar marginea laterală este egală cu 2 a. Aflați raza sferei circumscrise. Dat: AB=BC=AC=a, AA 1 ┴ABC ; AA 1= 2a. Găsiți: Rw = ? Rezolvare: 1)AB=AO √3; AO=a/√3. 2)R w =√ a 2 + a 2 /3=2a/ √ 3 Răspuns: 2a/ √ 3 C 1 B A 1 C B 1 A O w R w. O O 1

Consecințe. 1) Puteți descrie întotdeauna o sferă în jurul unei piramide triunghiulare, deoarece puteți descrie întotdeauna un cerc în jurul unui triunghi. 2) Puteți descrie oricând o sferă în jurul unei piramide obișnuite. 3) Dacă marginile laterale ale piramidei sunt egale (la fel de înclinate față de bază), atunci o sferă poate fi întotdeauna descrisă în jurul unei astfel de piramide. *În ultimele două cazuri, centrul sferei se află pe linia dreaptă care conține înălțimea piramidei. O. O.

Probleme (sfera descrisă lângă piramidă). În jurul piramidei PABC este descrisă o bilă, a cărei bază este un triunghi regulat ABC cu latura 4√3. Muchia laterală PA este perpendiculară pe planul bazei piramidei și este egală cu 6. Aflați raza bilei. Dat: AB=BC=AC=4 √3 ; PA ┴(ABC); PA=6. Găsiți: Rw = ? Rezolvare: 1) OO SF ┴(ABC); O – centrul unui cerc circumscris în jurul ∆ABC; K O SF ┴ PA; KP=AK (KO SF Una dintre perpendicularele medii pe marginea laterală PA); O SF este centrul sferei circumscrise. 2) OO SF┴(ABC); OO SF aparține (AKO); PA ┴(ABC); AK aparține lui (AKO); înseamnă KA|| OO SF; . O SF. O K. P. A. B. C

Probleme (sfera descrisă lângă piramidă). 3) KO c f ┴AP; KO c f aparține (AOK); AO┴AP; AO aparține lui (AOK); înseamnă KO c f || AO; 4) Din (2) și (3): AOO c f K- dreptunghi, AK=PA/2=3; 5) AO=AB/ √3 =4; 6) ∆ AO O c f: AO c f = R w =5 Răspuns: 5

Probleme (sfera descrisă lângă piramidă). Într-o piramidă patruunghiulară obișnuită, marginea laterală este înclinată față de bază la un unghi de 45˚. Înălțimea piramidei este h. Aflați raza sferei circumscrise. Dat: PABCD – piramidă regulată; (AP^(ABC))=45 ˚; PO=h. Găsiți: Rw = ? Rezolvare: 1) AO=OP=h; AP=h √ 2; 2) ∆PAP ​​​​1 – dreptunghiular; PP 1 – diametrul bilei; PP1 = 2 Rw; AP 2 = PP 1 *OP; (h √ 2) 2 =2 R w *h; Rw = 2h2/2h=h. Răspuns: h. C. B A. .D .P .P 1 . O

Sarcini (sfera descrisă lângă piramidă). Pe cont propriu. Raza unei sfere circumscrise unui tetraedru regulat este egală cu R. Aflați suprafața totală a tetraedrului.

Probleme (sfera descrisă lângă piramidă). Pe cont propriu. Dat: DABC – tetraedru regulat; R este raza sferei. Găsiți: S full tetra. =? Rezolvare: 1) Deoarece tetraedrul este regulat, centrul sferei circumscrise apartine dreptei ce contine inaltimea piramidei; 2) S full tetra. = a 2 √ 3/4*4= a 2 √ 3; 3) Punctele D, A, D 1 aparțin aceluiași cerc - secțiunea sferei după planul DAD 1, ceea ce înseamnă că unghiul DAD 1 este un unghi înscris pe baza diametrului, DD 1; unghi DAD 1 =90 ˚; 4) AO – înălțimea ∆ ADD 1 desenată din vârful unghiului drept. AD 2 = DO*DD 1 ; 5) AO=a/ √ 3; DO= √ a 2 -a 2 /3=a √ 2 / √ 3; a 2 = a √ 2 / √ 3*2R; a= √ 2 / √ 3*2R; a2 = 8R2/3; .D 1 .D .O .B .C A. a a

Probleme (sfera descrisă lângă piramidă). Pe cont propriu. 6) S full tet. = 8R 2 √ 3/3 Răspuns: 8R 2 √ 3/3