Как пишется три одиннадцатых в десятичных дробях. Составление системы уравнений
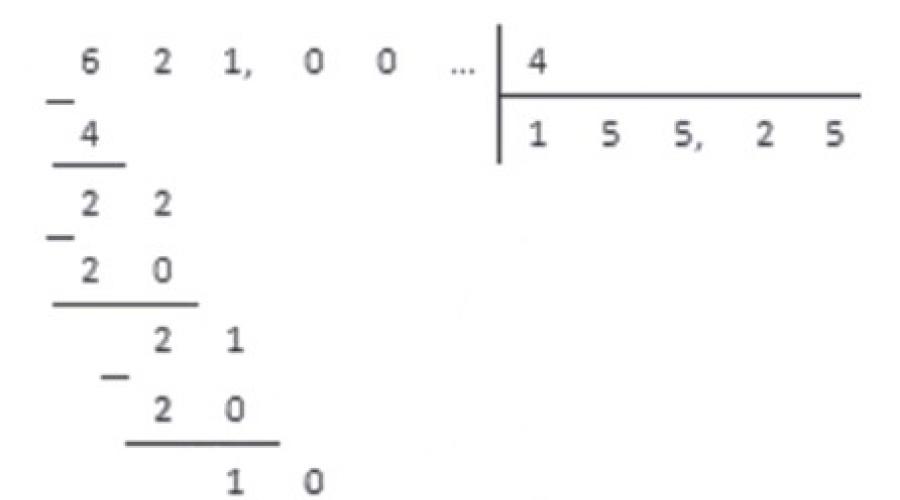
Читайте также
Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.
Yandex.RTB R-A-339285-1
Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.
Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.
Приступим!
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.
Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.
Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?
Правило перевода обыкновенных правильных дробей в десятичные
- Записываем 0 и ставим после него запятую.
- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Пример 1. Перевод обыкновенных дробей в десятичные
Переведем обыкновенную дробь 39 100 в десятичную.
Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно - количество цифр в числителе совпадает с количеством нулей в знаменателе.
Следуя правилу, записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 39 .
Разберем решение еще одного примера по этой теме.
Пример 2. Перевод обыкновенных дробей в десятичные
Запишем дробь 105 10000000 в виде десятичной дроби.
Количество нулей в знаменателе равно 7 , а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:
0000105 10000000
Теперь записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 0000105 .
Рассмотренные во всех примерах дроби - обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
Правило перевода обыкновенных неправильных дробей в десятичные
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Ниже приведем пример на использование этого правила.
Пример 3. Перевод обыкновенных дробей в десятичные
Переведем дробь 56888038009 100000 из обыкновенной неправильной в десятичную.
Сначала запишем число из числителя:
Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе - пять). Получим:
Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.
Правило перевода смешанных чисел в десятичные дроби
- Выполняем подготовку дробной части числа, если это необходимо.
- Записываем целую часть исходного числа и ставим после него запятую.
- Записываем число из числителя дробной части вместе с дописанными нулями.
Обратимся к примеру.
Пример 4. Перевод смешанных чисел в десятичные дроби
Переведем смешанное число 23 17 10000 в десятичную дробь.
В дробной части имеем выражение 17 10000 . Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 0017 10000 .
Теперь записываем целую часть числа и ставим после него запятую: 23 , . .
После запятой записываем число из числителя вместе с нулями. Получаем результат:
23 17 10000 = 23 , 0017
Перевод обыкновенных дробей в конечные и бесконечные периодические дроби
Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.
Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.
Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.
Числитель при делении представляется в виде десятичной дроби - справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.
Пример 5. Перевод обыкновенных дробей в десятичные
Переведем обыкновенную дробь 621 4 в десятичный вид.
Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621 = 621 , 00
Теперь разделим столбиком 621 , 00 на 4 . Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.
Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.

В итоге мы получаем десятичную дробь 155 , 25 , которая и является результатом обращения обыкновенной дроби 621 4
621 4 = 155 , 25
Рассмотрим решение еще одного примера, чтобы закрепить материал.
Пример 6. Перевод обыкновенных дробей в десятичные
Обратим обыкновенную дробь 21 800 .
Для этого в столбик разделим дробь 21 , 000 на 800 . Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.

В результате мы получили: 21 800 = 0 , 02625 .
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
Пример 7. Перевод обыкновенных дробей в десятичные
Обратим обыкновенную дробь 19 44 в десятичную. Для этого выполним деление столбиком.

Мы видим, что при делении повторяются остатки 8 и 36 . При этом в частном повторяются цифры 1 и 8 . Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.
Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.
19 44 = 0 , 43 (18) .
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие - в бесконечные периодические?
Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.., то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.
Подытожим сказанное:
- Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
- Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.
Приведем пример.
Пример 8. Перевод обыкновенных дробей в десятичные
Какая из данных дробей 47 20 , 7 12 , 21 56 , 31 17 переводится в конечную десятичную дробь, а какая - только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.
Дробь 47 20 , как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100 .
47 20 = 235 100 . Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.
Разложение знаменателя дроби 7 12 на множители дает 12 = 2 · 2 · 3 . Так как простой множитель 3 отличен от 2 и от 5 , данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.
Дробь 21 56 , во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 3 8 , разложение знаменателя которой на множители дает 8 = 2 · 2 · 2 . Следовательно, это конечная десятичная дробь.
В случае с дробью 31 17 разложение знаменателя на множители представляет собой само простое число 17 . Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.
Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь
Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?
Отвечаем: нет!
Важно!
При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.
Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:
- Мы получаем в остатке 0, и на этом деление заканчивается.
- Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.
Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
Правило перевода десятичных дробей в обыкновенные дроби
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Пример 8. Перевод десятичных дробей в обыкновенные
Представим число 3 , 025 в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
- В знаменателе пишем единицу, а после нее три нуля - именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
- Полученную дробь 3025 1000 можно сократить на 25 , в результате чего мы получим: 3025 1000 = 121 40 .
Пример 9. Перевод десятичных дробей в обыкновенные
Переведем дробь 0 , 0017 из десятичных в обыкновенные.
- В числителе запишем дробь 0 , 0017 , отбросив запятую и нули слева. Получится 17 .
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000 . Данная дробь несократима.
Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
Правило перевода десятичных дробей в смешанные числа.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Пример 10. Перевод десятичной дроби в смешанное число
Представим дробь 155 , 06005 в виде смешанного числа.
- Записываем число 155 , как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число: 155 6005 100000
Дробную часть можно сократить на 5 . Сокращаем, и получаем финальный результат:
155 , 06005 = 155 1201 20000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай - период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример 11. Перевод периодической десятичной дроби в обыкновенную
Обратим периодическую дробь 3 , 75 (0) .
Отбросив нули справа, получим конечную десятичную дробь 3 , 75 .
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
3 , 75 (0) = 3 , 75 = 375 100 = 15 4 .
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
0 , (74) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b , а знаменатель q таков, что 0 < q < 1 , то сумма равна b 1 - q .
Рассмотрим несколько примеров с применением данной формулы.
Пример 12. Перевод периодической десятичной дроби в обыкновенную
Пусть у нас есть периодическая дробь 0 , (8) и нам нужно перевести ее в обыкновенную.
0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . .
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0 , 8 и знаменателем 0 , 1 .
Применим формулу:
0 , (8) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 - 0 , 1 = 0 , 8 0 , 9 = 8 9
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Пример 13. Перевод периодической десятичной дроби в обыкновенную
Обратим дробь 0 , 43 (18) .
Сначала записываем дробь в виде бесконечной суммы:
0 , 43 (18) = 0 , 43 + (0 , 0018 + 0 , 000018 + 0 , 00000018 . .)
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 - 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .
Полученное прибавляем к конечной дроби 0 , 43 = 43 100 и получаем результат:
0 , 43 (18) = 43 100 + 18 9900
После сложения данных дробей и сокращения получим окончательный ответ:
0 , 43 (18) = 19 44
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Из множества дробей, встречающихся в арифметике, отдельного внимания заслуживают такие, у которых в знаменателе стоит 10, 100, 1000 - в общем, любая степень десятки. У этих дробей есть специальное название и форма записи.
Десятичная дробь - это любая числовая дробь, в знаменателе которой стоит степень десятки.
Примеры десятичных дробей:
Зачем вообще потребовалось выделять такие дроби? Почему для них нужна собственная форма записи? На то есть как минимум три причины:
- Десятичные дроби намного удобнее сравнивать. Вспомните: для сравнения обычных дробей их требуется вычесть друг из друга и, в частности, привести дроби к общему знаменателю. В десятичных дробях ничего подобного не требуется;
- Сокращение вычислений. Десятичные дроби складываются и умножаются по собственным правилам, и после небольшой тренировки вы будете работать с ними намного быстрее, чем с обычными;
- Удобство записи. В отличие от обычных дробей, десятичные записываются в одну строчку без потери наглядности.
Большинство калькуляторов также дают ответы именно в десятичных дробях. В некоторых случаях другой формат записи может привести к проблемам. Например, что, если потребовать в магазине сдачу в размере 2/3 рубля:)
Правила записи десятичных дробей
Основное преимущество десятичных дробей - удобная и наглядная запись. А именно:
Десятичная запись - это форма записи десятичных дробей, где целая часть отделяется от дробной с помощью обычной точки или запятой. При этом сам разделитель (точка или запятая) называется десятичной точкой.
Например, 0,3 (читается: «ноль целых, 3 десятых»); 7,25 (7 целых, 25 сотых); 3,049 (3 целых, 49 тысячных). Все примеры взяты из предыдущего определения.
На письме в качестве десятичной точки обычно используется запятая. Здесь и далее на всем сайте тоже будет использоваться именно запятая.
Чтобы записать произвольную десятичную дробь в указанной форме, надо выполнить три простых шага:
- Выписать отдельно числитель;
- Сдвинуть десятичную точку влево на столько знаков, сколько нулей содержит знаменатель. Считать, что изначально десятичная точка стоит справа от всех цифр;
- Если десятичная точка сдвинулась, а после нее в конце записи остались нули, их надо зачеркнуть.
Бывает, что на втором шаге у числителя не хватает цифр для завершения сдвига. В этом случае недостающие позиции заполняются нулями. Да и вообще, слева от любого числа можно без ущерба для здоровья приписывать любое количество нулей. Это некрасиво, но иногда полезно.
На первый взгляд, данный алгоритм может показаться довольно сложным. На самом деле все очень и очень просто - надо лишь немного потренироваться. Взгляните на примеры:
Задача. Для каждой дроби укажите ее десятичную запись:
Числитель первой дроби: 73. Сдвигаем десятичную точку на один знак (т.к. в знаменателе стоит 10) - получаем 7,3.
Числитель второй дроби: 9. Сдвигаем десятичную точку на два знака (т.к. в знаменателе стоит 100) - получаем 0,09. Пришлось дописать один ноль после десятичной точки и еще один - перед ней, чтобы не оставлять странную запись вида «,09».
Числитель третьей дроби: 10029. Сдвигаем десятичную точку на три знака (т.к. в знаменателе стоит 1000) - получим 10,029.
Числитель последней дроби: 10500. Снова сдвигаем точку на три знака - получим 10,500. В конце числа образовались лишние нули. Зачеркиваем их - получаем 10,5.
Обратите внимание на два последних примера: числа 10,029 и 10,5. Согласно правилам, нули справа надо зачеркнуть, как это сделано в последнем примере. Однако ни в коем случае нельзя поступать так с нулями, стоящими внутри числа (которые окружены другими цифрами). Именно поэтому мы получили 10,029 и 10,5, а не 1,29 и 1,5.
Итак, с определением и формой записи десятичных дробей разобрались. Теперь выясним, как переводить обычные дроби в десятичные - и наоборот.
Переход от обычных дробей к десятичным
Рассмотрим простую числовую дробь вида a /b . Можно воспользоваться основным свойством дроби и умножить числитель и знаменатель на такое число, чтобы внизу получилась степень десятки. Но прежде, чем это делать, прочитайте следующее:
Существуют знаменатели, которые не приводятся к степени десятки. Учитесь распознавать такие дроби, потому что с ними нельзя работать по алгоритму, описанному ниже.
Вот такие дела. Ну и как понять, приводится знаменатель к степени десятки или нет?
Ответ прост: разложите знаменатель на простые множители. Если в разложении присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 - что угодно), о степени десятки можно забыть.
Задача. Проверить, можно ли представить указанные дроби в виде десятичных:
Выпишем и разложим на множители знаменатели этих дробей:
20 = 4 · 5 = 2 2 · 5 - присутствуют только числа 2 и 5. Следовательно, дробь можно представить в виде десятичной.
12 = 4 · 3 = 2 2 · 3 - есть «запретный» множитель 3. Дробь не представима в виде десятичной.
640 = 8 · 8 · 10 = 2 3 · 2 3 · 2 · 5 = 2 7 · 5. Все в порядке: кроме чисел 2 и 5 ничего нет. Дробь представима в виде десятичной.
48 = 6 · 8 = 2 · 3 · 2 3 = 2 4 · 3. Снова «всплыл» множитель 3. Представить в виде десятичной дроби нельзя.
Итак, со знаменателем разобрались - теперь рассмотрим весь алгоритм перехода к десятичным дробям:
- Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
- Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
- Собственно, умножить числитель и знаменатель исходной дроби на этот множитель - получим искомое представление, т.е. в знаменателе будет стоять степень десятки.
Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом, чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.
И еще: если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную - и только затем применяйте описанный алгоритм.
Задача. Перевести данные числовые дроби в десятичные:
Разложим на множители знаменатель первой дроби: 4 = 2 · 2 = 2 2 . Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен 5 2 = 25. С ним количество двоек и пятерок сравняется. Имеем:
Теперь разберемся со второй дробью. Для этого заметим, что 24 = 3 · 8 = 3 · 2 3 - в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.
Две последних дроби имеют знаменатели 5 (простое число) и 20 = 4 · 5 = 2 2 · 5 соответственно - везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором - 5. Получаем:
Переход от десятичных дробей к обычным
Обратное преобразование - от десятичной формы записи к обычной - выполняется намного проще. Здесь нет ограничений и специальных проверок, поэтому перевести десятичную дробь в классическую «двухэтажную» можно всегда.
Алгоритм перевода следующий:
- Зачеркните все нули, стоящие в десятичной дроби слева, а также десятичную точку. Это будет числитель искомой дроби. Главное - не переусердствуйте и не зачеркните внутренние нули, окруженные другими цифрами;
- Подсчитайте, сколько знаков стоит в исходной десятичной дроби после запятой. Возьмите цифру 1 и припишите справа столько нулей, сколько знаков вы насчитали. Это будет знаменатель;
- Собственно, запишите дробь, числитель и знаменатель которой мы только что нашли. По возможности, сократите. Если в исходной дроби присутствовала целая часть, сейчас мы получим неправильную дробь, что очень удобно для дальнейших вычислений.
Задача. Перевести десятичные дроби в обычные: 0,008; 3,107; 2,25; 7,2008.
Зачеркнем нули слева и запятые - получим следующие числа (это будут числители): 8; 3107; 225; 72008.
В первой и во второй дробях после запятой стоит по 3 знака, во второй - 2, а в третьей - целых 4 знака. Получим знаменатели: 1000; 1000; 100; 10000.
Наконец, объединим числители и знаменатели в обычные дроби:

Как видно из примеров, полученную дробь очень часто можно сократить. Еще раз отмечу, что любая десятичная дробь представима в виде обычной. Обратное преобразование можно выполнить не всегда.
Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.
Yandex.RTB R-A-339285-1
Что такое десятичная запись дробных чисел
Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.
Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.
Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.
В некоторых учебниках можно встретить использование точки вместо запятой (5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.
Определение десятичных дробей
Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:
Определение 1
Десятичные дроби представляют собой дробные числа в десятичной записи.
Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .
О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.
Как правильно читать десятичные дроби
Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».
Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».
Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.
Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:
Разберем пример.
Пример 1
У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .
Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.
Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.
Пример 2
Попробуем разложить дробь 56 , 0455 по разрядам.
У нас получится:
56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005
Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.
Что такое конечные десятичные дроби
Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:
Определение 1
Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.
Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.
Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)
Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Определение 2
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Определение 3
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .
Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , (4) , а 76 , 134134134134 … – как 76 , (134) .
В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 (7) и 0 , 6 (77) и т.д. Также допустимы записи вида 0 , 67777 (7) , 0 , 67 (7777) и др.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
То есть для указанной выше дроби основной будем считать запись 0 , 6 (7) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 (34) .
Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.
В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 (0) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.
Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 (9) , 31 , 6 (9) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.
К примеру, дробь 8 , 31 (9) можно заменить на соответствующую ей дробь 8 , 32 (0) . Или 4 , (9) = 5 , (0) = 5 .
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
Определение 4
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Основные действия с десятичными дробями
С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.
Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.
Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.
Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.
Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.
Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.
Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.
Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .
Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.
Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.
Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.
Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .
Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В данной статье мы с Вами разберемся, что такое десятичная дробь, какие у нее есть особенности и свойства. Поехали! 🙂
Десятичная дробь является частным случаем обыкновенных дробей (у которой знаменатель кратен 10).
Определение
Десятичными называют дроби, знаменатели которых представляют собой числа, состоящие из единицы и некоторого количества следующих за нею нулей. То есть это дроби со знаменателем 10, 100, 1000 и т.д. Иначе десятичную дробь можно охарактеризовать как дробь со знаменателем 10 или одной из степеней десятки.
Примеры дробей:
, ,
Десятичная дробь записывается иначе, чем обыкновенная. Операции с этими дробями также отличны от операций с обыкновенными. Правила действий над ними в значительной мере приближены к правилами действий над целыми числами. Этим, в частности, обусловлена их востребованность при решении практических задач.
Представление дроби в десятичной записи
В записи десятичной дроби нет знаменателя, в ней отображено число числителя. В общем виде запись десятичной дроби осуществляется по такой схеме:
где Х – целая часть дроби, Y – ее дробная часть, «,» – десятичная запятая.
Для правильного представления обыкновенной дроби в виде десятичной требуется, чтобы она была правильной, то есть с выделенной целой частью (если это возможно) и числителем, который меньше знаменателя. Тогда в десятичной записи целая часть записывается до десятичной запятой (Х), а числитель обыкновенной дроби – после десятичной запятой (Y).
Если в числителе представлено число с количеством знаков, меньшим, чем количество нулей в знаменателе, то в части Y недостающее количество знаков в десятичной записи заполняется нулями впереди цифр числителя.
Пример:![]()
Если обыкновенная дробь меньше 1, т.е. не имеет целой части, то для Х в десятичном виде записывают 0.
В дробной части (Y), после последнего значимого (отличного от нуля) разряда, может быть вписано произвольное количество нулей. На значение дроби это не влияет. И наоборот: все нули в конце дробной части десятичной дроби можно опустить.
Прочтение десятичных дробей
Часть Х читается в общем случае так: «Х целых».
Часть Y прочитывается в соответствии с числом в знаменателе. Для знаменателя 10 следует читать: «Y десятых», для знаменателя 100: «Y сотых», для знаменателя 1000: «Y тысячных» и так далее… 😉
Более корректным считается другой подход к прочтению, основанный на подсчете количества разрядов дробной части. Для этого нужно понимать, что дробные разряды расположены в зеркальном отражении по отношению к разрядам целой части дроби.
Наименования для правильного прочтения приведены в таблице:

Исходя из этого, прочтение должно опираться на соответствие наименованию разряда последней цифры дробной части.
- 3,5 читается как «три целых пять десятых»
- 0,016 читается как «ноль целых шестнадцать тысячных»
Перевод произвольной обыкновенной дроби в десятичную
Если в знаменателе обыкновенной дроби стоит 10 или какая-нибудь степень десятки, то перевод дроби выполняется как описано выше. В остальных ситуациях необходимы дополнительные преобразования.
Существует 2 способа перевода.
Первый способ перевода
Числитель и знаменатель необходимо домножить на такое целое число, чтобы в знаменателе было получено число 10 или одна из степеней десятки. А далее дробь представляется в десятичной записи.
Этот способ применим для дробей, знаменатель которых раскладывается только на 2 и 5. Так, в предыдущем примере ![]() . Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
. Если же в разложении присутствуют другие простые множители (например, ), то придется прибегнуть ко 2-му способу.
Второй способ перевода
2-й способ заключается в делении числителя на знаменатель в столбик или на калькуляторе. Целая часть, если таковая имеется, в преобразовании не участвует.
Правило деления в столбик, приводящее в результате к десятичной дроби, описано ниже (см. Деление десятичных дробей).
Перевод десятичной дроби в обыкновенную
Для этого следует ее дробную часть (справа от запятой) записать в виде числителя, а результат прочтения дробной части – в виде соответствующего числа в знаменателе. Далее, если это возможно, нужно сократить полученную дробь.
![]()
Конечная и бесконечная десятичная дробь
Конечной называют десятичная дробь, дробная часть которой состоит из конечного количества цифр.
Выше все приведенные примеры содержат именно конечные десятичные дроби. Однако не всякую обыкновенную дробь возможно представить в виде конечной десятичной. Если 1-й способ перевода для данной дроби не применим, а 2-й способ демонстрирует, что деление невозможно завершить, значит, получена может быть только бесконечная десятичная дробь.
В полном виде бесконечную дробь записать невозможно. В неполном же виде такие дроби можно представить:
- как результат сокращения до желательного количества разрядов после запятой;
- в виде периодической дроби.
Периодической называется дробь, у которой после запятой можно выделить повторяющуюся бесконечно последовательность цифр.
Остальные дроби называются непериодическими. Для непериодических дробей допустим только 1-й способ представления (округление).
Пример периодической дроби: 0,8888888… Здесь налицо повторяющаяся цифра 8, которая, очевидно, будет повторяться до бесконечности, поскольку нет оснований предполагать иное. Эта цифра называется периодом дроби .
Периодические дроби бывают чистыми и смешанными. Чистой является десятичная дробь, у которой период начинается непосредственно после запятой. У смешанной дроби до периода после запятой имеется 1 или больше цифр.
54,33333… – периодическая чистая десят.дробь
2,5621212121… – периодическая смешанная дробь
Примеры записи бесконечных десятичных дробей:
Во 2-м примере показано, как правильно оформлять период в записи периодической дроби.
Перевод периодических десятичных дробей в обыкновенные
Для перевода чистой периодической дроби в обыкновенную ее период записывают в числитель, а в знаменатель пишут число, состоящее из девяток в количестве, равном количеству цифр в периоде.
![]()
Смешанная периодическая десятичная дробь переводится следующим образом:
- нужно сформировать число, состоящее из числа, стоящего после запятой до периода, и первого периода;
- из полученного числа вычесть число, стоящее после запятой до периода. Итог составит числитель обыкновенной дроби;
- в знаменателе требуется вписать число, состоящее из кол-ва девяток, равных кол-ву цифр периода, а за ними нулей, кол-во которых равно количеству цифр числа, стоящего после запятой до 1-го периода.
![]()
![]()
Сравнение десятичных дробей
Десятичные дроби сравнивают первоначально по их целым частям. Больше та дробь, у которой больше ее целая часть.
Если целые части одинаковы, то сравнивают цифры соответствующих разрядов дробной части, начиная с первого (с десятых). Здесь действует тот же принцип: больше та из дробей, у которой больше разряд десятых; при равенстве цифр разряда десятых сравнивают разряды сотых и так далее.
Поскольку
![]() , поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
, поскольку при равных целых частях и равных десятых в дробной части у 2-й дроби больше цифра сотых.
Сложение и вычитание десятичных дробей
Десятичные дроби складывают и вычитают так же, как и целые числа, записав соответствующие цифры друг под другом. Для этого нужно, чтобы друг под другом находились десятичные запятые. Тогда единицы (десятки и т.д.) целой части, а также десятые (сотые и т.д.) дробной окажутся в соответствии. Недостающие разряды дробной части заполняют нулями. Непосредственно процесс сложения и вычитания осуществляется так же, как и для целых чисел.
Умножение десятичных дробей
Для умножения десятичных дробей нужно записать их друг под другом, выровняв по последней цифре и не обращая внимания на местоположение десятичных запятых. Затем нужно перемножить числа так же, как и при умножении целых чисел. После получения результата следует пересчитать количество цифр после запятой в обоих дробях и отделить запятой в результирующем числе суммарное количество дробных разрядов. Если разрядов не хватает, то они заменяются нулями.

Умножение и деление десятичных дробей на 10 n
Эти действия просты и сводятся к переносу десятичной запятой. При умножении запятая переносится вправо (дробь увеличивается) на количество знаков, равных количеству нулей в 10 n , где n – произвольная целая степень. То есть некоторое количество цифр переносится из дробной части в целую. При делении, соответственно, запятая переносится влево (число уменьшается), и некоторая часть цифр переносится из целой части в дробную. Если цифр для переноса оказывается недостаточно, то недостающие разряды заполняются нулями.
Деление десятичной дроби и целого числа на целое число и на десятичную дробь
Деление в столбик десятичной дроби на целое число выполняется аналогично делению двух целых чисел. Дополнительно требуется только учет положения десятичной запятой: при сносе цифры разряда, за которым следует запятая, необходимо поставить запятую после текущей цифры формируемого ответа. Далее нужно продолжать делить до получения нуля. Если знаков в делимом для полного деления недостает, в их качестве следует использовать нули.

Аналогично делятся в столбик 2 целых числа, если снесены все цифры делимого, а полное деление еще не завершено. В этом случае после сноса последней цифры делимого ставится десят.запятая в формирующемся ответе, а в качестве сносимых цифр используют нули. Т.е. делимое здесь, по сути, представляют как десятичную дробь с нулевой дробной частью.

Для деления десят.дроби (или целого числа) на десят.число необходимо домножить делимое и делитель на число 10 n , в котором количество нулей равно количеству цифр после десят.запятой в делителе. Таким способом избавляются от десят.запятой в дроби, на которую требуется делить. Далее процесс деления совпадает с описанным выше.
Графическое представление десятичных дробей
Графически десятичные дроби изображаются посредством координатной прямой. Для этого единичные отрезки делят дополнительно на 10 равных долей подобно тому, как на линейке откладываются одновременно сантиметры и миллиметры. Это обеспечивает точное отображение десятичных дробей и возможность объективного их сравнения.
Чтобы дольные деления на единичных отрезках были одинаковыми, следует тщательно продумывать длину самого единичного отрезка. Она должна быть такой, чтобы можно было обеспечить удобство дополнительного деления.
Дроби записанные в форме 0,8; 0,13; 2,856; 5,2; 0,04 называют десятичными. На самом деле десятичные дроби это упрощенная запись обычных дробей. Эту запись удобно использовать для всех дробей, у которых знаменатели равны 10, 100, 1000 и так далее.
Рассмотрим примеры (0,5 читают как, ноль целых пять десятых);
 (0,15 читают как, ноль целых пятнадцать сотых);
(0,15 читают как, ноль целых пятнадцать сотых);
 (5,3 читают как, пять целых три десятых).
(5,3 читают как, пять целых три десятых).
Обратим внимание, что в записи десятичной дроби запятая отделяет целую часть числа от дробной, целая часть правильной дроби рана 0. Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.
Рассмотрим пример,  ,
,  ,
,  .
.
В некоторых случаях бывает необходимо рассматривать натуральное число как десятичную дробь, у которой дробная часть равна нулю. Принято записывать что, 5 = 5,0; 245 = 245,0 и так далее. Заметим, что в десятичной записи натурального числа единица младшего разряда в 10 раз меньше единицы соседнего старшего разряда. Таким же свойством обладает запись десятичных дробей. Поэтому сразу после запятой идет разряд десятых, далее разряд сотых, затем разряд тысячных и так далее. Ниже приведены названия разрядов числа 31,85431 первые два столбца — целая часть, остальные столбцы — дробная часть.

Читается эта дробь как тридцать одна целая восемьдесят пять тысяч четыреста тридцать одна стотысячная.
Сложение и вычитание десятичных дробей
Первый способ, это обратить десятичные дроби в обыкновенные и произвести сложение.
как видно из примера этот способ очень неудобный и лучше воспользоваться вторым способом более правильным, не обращая десятичные дроби в обыкновенные. Для того чтобы сложить две десятичные дроби, надо:
- уравнять в слагаемых количество цифр после запятой;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми в слагаемых.
Рассмотрим примеры:
- уравнять в уменьшаемом и вычитаемом количество цифр после запятой;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- произвести вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.
Рассмотрим примеры:
В рассмотренных выше примерах видно, что сложение и вычитание десятичных дробей выполнялось поразрядно, то есть так, как мы производили аналогичные действия с натуральными числами. Это и есть главное преимущество десятичной формы записи дробей.
Умножение десятичных дробей
Для того чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и так далее цифры. Следовательно, если запятую перенести вправо на 1, 2, 3 и так далее цифры, то дробь увеличится соответственно в 10, 100, 1000 и так далее раз. Для того чтобы перемножить две десятичные дроби, надо:
- умножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Встречаются случаи, когда произведение содержит меньше цифр, чем требуется отделить запятой, слева перед этим произведением дописывают необходимое количество нулей, а затем переносят запятую влево на нужное количество цифр.
Рассмотрим примеры: 2 * 4 = 8, тогда 0,2 * 0,4 = 0,08; 23 * 35 = 805, тогда 0,023 * 0,35 = 0,00805.
Встречаются случаи, когда один из множителей равен 0,1; 0,01; 0,001 и так далее, удобнее пользоваться следующим правилом.
- Для того чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и так далее, надо в этой десятичной дроби перенести запятую влево соответственно на 1, 2, 3 и так далее цифры.
Рассмотрим примеры: 2,65 * 0,1 = 0,265; 457,6 * 0,01 = 4,576.
Свойства умножения натуральных чисел выполняются и для десятичных дробей.
- ab = ba — переместительное свойство умножения;
- (ab) c = a (bc) — сочетательное свойство умножения;
- a (b + c) = ab + ac — распределительное свойство умножения, относительно сложения.
Деление десятичных дробей
Известно, если разделить натуральное число a на натуральное число b означает найти такое натуральное число c , которое при умножении на b дает число a . Это правило остается верным, если хотя бы одно из чисел a, b, c является десятичной дробью.
Рассмотрим пример, требуется разделить 43,52 на 17 уголком, не обращая внимания на запятую. При этом запятую в частном следует поставить непосредственно перед тем, как будет использована первая цифра после запятой в делимом.
Бывают случаи когда делимое меньше делителя, тогда целая часть частного равна нулю. Рассмотрим пример:
Рассмотрим еще один интересный пример.
Процесс деления остановлен, потому что цифры делимого закончились, а в остатке нуль не получили. Известно, что десятичная дробь не изменится, если к ней справа приписать любое количество нулей. Тогда становится понятно, что цифры делимого закончится не могут.
Для того чтобы разделить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую влево на 1, 2, 3 и так далее цифры. Рассмотрим пример: 5,14: 10 = 0,514; 2: 100 = 0,02; 37,51: 1000 = 0,03751.
Если делимое и делитель увеличить одновременно в 10, 100, 1000 и так далее раз, то частное не изменится.
Рассмотрим пример: 39,44: 1,6 = 24,65 увеличим делимое и делитель в 10 раз 394,4: 16 = 24,65 справедливо заметить, что делить десятичную дробь на натуральное число во втором примере легче.
Для того чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Рассмотрим пример: 23,6: 0,02 заметим, что в делителе стоит два знака после запятой, следовательно умножаем оба числа на 100 получаем 2360: 2 = 1180 делим результат на 100 и получаем ответ 11,80 или 23,6: 0,02 = 11,8.
Сравнение десятичных дробей
Существует два способа сравнения десятичных дробей. Способ первый, требуется сравнить две десятичные дроби 4,321 и 4,32 уравниваем количество знаков после запятой и начинаем сравнивать поразрядно, десятые с десятыми, сотые с сотыми и так далее в итоге получаем 4,321 > 4,320.
Второй способ сравнения десятичных дробей производится с помощью умножения, умножим вышеприведенный пример на 1000 и сравним 4321 > 4320. Какой способ удобней, каждый выбирает для себя сам.