Trouvez le diamètre en couple. Calculs de résistance et de rigidité en torsion
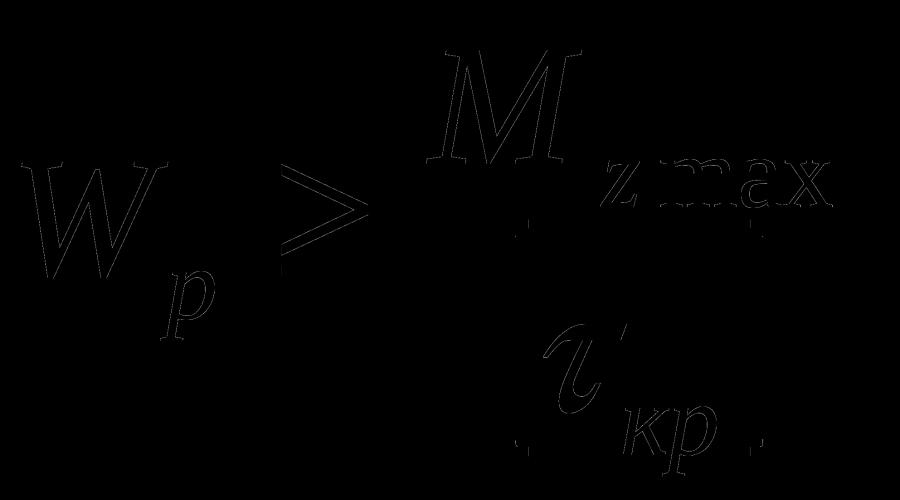
Lire aussi
TORSION
Séquence de résolution du problème
1. Déterminer les moments de torsion externes à l'aide de la formule
M=P/ω
Où R. - pouvoir,
ω - vitesse angulaire.
2. Puisqu'avec une rotation uniforme de l'arbre, la somme algébrique des moments de torsion (rotation) externes qui lui sont appliqués est égale à zéro, déterminez le moment d'équilibrage à l'aide de l'équation d'équilibre
∑ M je z = 0
3. À l'aide de la méthode des sections, construisez un diagramme des couples sur toute la longueur de l'arbre.
4. Pour la section de l'arbre dans laquelle le couple le plus important se produit, déterminez le diamètre de l'arbre à section ronde ou annulaire en fonction des conditions de résistance et de rigidité. Pour la section annulaire de l'arbre, prendre le rapport des diamètres
Où d Ô- diamètre intérieur de la bague ;
d - diamètre extérieur de la bague.
De la condition de résistance :
A partir de la condition de rigidité :


Où M zmax- couple maximal;
W p - moment de torsion polaire ;
[τ cr] - contrainte de cisaillement admissible
Où J. p - moment d'inertie polaire de la section ;
g - module d'élasticité en cisaillement ;
[φ Ô] - angle de torsion admissible de la section
Section transversale de l'arbre - cercle


Diamètre d'arbre requis pour la résistance :
Diamètre d'arbre requis pour la rigidité :


Section d'arbre - bague


Diamètre de bague extérieure de résistance requise :
Rigidité requise diamètre extérieur de la bague :


Exemple 1 . Pour un arbre en acier (Fig. 1) à section constante sur la longueur, il faut : 1) déterminer les valeurs des moments M 2 Et M 3 , correspondant aux puissances transmises R. 2 Et R. 3 , ainsi que le moment d'équilibrage M 1 ; 2) construire un diagramme de couples ; 3) déterminer le diamètre d'arbre requis à partir de calculs de résistance et de rigidité, en supposant l'option (UN) (b) - c =d 0 /d=0,8.
Accepter: [ τ cr ] = 30 MPa ; [ φ 0 ] = 0,02 rad/m ; R. 2 = 52 kW ; R. 3 = 50 kW ; ω = 20 rad/s ; g = 8 10 4 MPa

Riz. 1 - Diagramme du problème
Solution:
1. Déterminer les moments de torsion externes :
M 2 = P 2 / ω = 52 10 3 / 20 = 2600 N m
M 3 = P 3 / ω = 50 10 3 / 20 = 2500 N m
2. Déterminer le moment d'équilibrage M 1 :
∑ M je z = 0 ; M1 – M2 – M3 =0
M 1 =M 2 +M 3 = 5100 Nm
3. Déterminez le couple par sections de l'arbre :
M z je= M 1 = 5 100 N m
M z II= M1 – M2 = 5100 – 2600 = 2500 N m
Nous construisons un diagramme de couples Mz(Fig.2).

Riz. 2 - Diagramme de couple
4. Nous déterminons le diamètre de l'arbre à partir des conditions de résistance et de rigidité, en prenantM z maximum = 5100N m(Fig.2).
a) Section d'arbre – cercle.
De la condition de résistance :
Nous acceptons d = 96mm
A partir de la condition de rigidité :
Nous acceptons d = 76mm
Le diamètre requis s'est avéré plus grand en fonction de la résistance, nous l'acceptons donc comme d final = 96 mm.
b) La section transversale de l'arbre est un anneau.
De la condition de résistance :
Nous acceptons d = 114 mm
A partir de la condition de rigidité :
Nous acceptons d = 86mm
Les diamètres requis sont finalement issus des calculs de résistance :
Diamètre extérieur de la bague d = 114 mm
Diamètre intérieur du piquet tsa d Ô = 0,8 d = 0,8 114 = 91,2 mm. Nous acceptons d Ô =92mm .
Tache 1. Pour un arbre en acier (Fig. 3) de section constante il faut : 1) déterminer les valeurs des moments M 1 , M 2 , M 3 Et M 4 ; 2) construire un diagramme de couples ; 3) déterminer le diamètre de l'arbre à partir de calculs de résistance et de rigidité, en supposant selon l'option (UN) la section transversale de l'arbre est un cercle ; selon option (b)- section transversale de l'arbre - une bague ayant un rapport de diamètre c =d 0 /d=0,7. Prise de puissance des engrenages R. 2 = 0,5R 1 ; R. 3 = 0,3Р 1 ; R. 4 = 0,2Р 1 .
Accepter: [ τ cr ] = 30 MPa ; [ φ 0 ] = 0,02 rad/m ; g = 8 10 4 MPa
Arrondissez la valeur finale du diamètre au nombre pair le plus proche (ou se terminant par cinq).
Prenez les données pour votre option dans le tableau 1
Note: Arrondissez la valeur de diamètre calculée obtenue (en mm) au nombre le plus proche se terminant par 0, 2, 5, 8.
Tableau 1 - Données initiales
Numéro du programme dans la figure 3.2.5
P1
Possibilités
rad/s
kW

Riz. 3 - Diagramme du problème
Exercice
Pour un arbre en acier de section circulaire, déterminer les valeurs des moments extérieurs correspondant aux puissances transmises et au moment d'équilibre (Tableau 7.1 et Tableau 7.2).
Construisez un diagramme des couples sur toute la longueur de l’arbre.
Déterminez les diamètres d'arbre par section transversale en fonction des calculs de résistance et de rigidité. Arrondissez le résultat le plus grand obtenu au nombre pair le plus proche ou se terminant par 5.
Lors du calcul, utilisez les données suivantes : l'arbre tourne à une vitesse angulaire de 25 rad/s ; matériau de l'arbre - acier, contrainte de torsion admissible 30 MPa, module d'élasticité en cisaillement 8 10 4 MPa ; angle de torsion admissible = 0,02 rad/m.
Effectuer les calculs pour un arbre de section annulaire en prenant Avec= 0,9. Tirer des conclusions sur l'opportunité de réaliser un arbre à section ronde ou annulaire en comparant les surfaces de section.
But du travail - apprendre à effectuer des calculs de conception et de vérification de poutres rondes pour des systèmes statiquement déterminés et à tester la rigidité.
Contexte théorique
La torsion est une charge dans laquelle un seul facteur de force interne apparaît dans la section transversale de la poutre : le couple. Les charges externes sont également deux paires de forces dirigées de manière opposée.
Répartition des contraintes tangentielles sur une section lors de la torsion (Fig. 7.1)
Contrainte de cisaillement en un point UN:

Figure 7.1
 (7.1)
(7.1)
où est la distance du point UN avant
centre de la tranche.
Condition de résistance à la torsion
![]() ;
; ![]() (cercle), (7.2)
(cercle), (7.2)
![]() (anneau), (7.3)
(anneau), (7.3)
où M k est le couple dans la section, N-m, N-mm ;
Wp- moment résistant à la torsion, m 3, mm 3 ;
[t k] - contrainte de torsion admissible, N/m 2, N/mm 2.
Calcul de conception, détermination des dimensions de la section
 (7.4)
(7.4)
Où d- diamètre extérieur de la section circulaire ;
d B n- diamètre intérieur de la section annulaire ; c = dBK /d.
Détermination de l'emplacement rationnel de l'arbre de roue
La disposition rationnelle des roues est une disposition dans laquelle la valeur maximale du couple sur l'arbre est la plus petite possible.
Condition de rigidité en torsion
; G ≈ 0,4E(7.5)
Où g- module d'élasticité en cisaillement, N/m 2, N/mm 2 ;
E- module d'élasticité en traction, N/m 2, N/mm 2.
[φо] - angle de torsion admissible, [φо] = 0,54-1 deg/m ;
Jp- moment d'inertie polaire dans la section, m 4, mm 4.
 (7.6) (7.6)
|
Calcul de conception, détermination du diamètre extérieur de la section
Demande de service
1. Construisez un diagramme des couples sur toute la longueur de l’arbre pour le circuit proposé dans la tâche.
2. Sélectionnez une disposition rationnelle des roues sur l'arbre et effectuez d'autres calculs pour un arbre avec des poulies judicieusement situées.
3. Déterminez les diamètres requis d'un arbre circulaire en fonction de la résistance et de la rigidité et sélectionnez la plus grande des valeurs obtenues, en arrondissant le diamètre.
4. Comparez les coûts du métal dans le cas de sections circulaires et annulaires. La comparaison est effectuée sur la base des sections transversales des arbres.
Questions de contrôle
1. Quelles déformations se produisent lors de la torsion ?
2. Quelles hypothèses sont vraies pour la déformation en torsion ?
3. La longueur et le diamètre de l'arbre changent-ils après la torsion ?
4. Quels facteurs de force internes apparaissent lors de la torsion ?
5. Quelle est la disposition rationnelle des oreilles sur la tige ?
6. Quel est le moment d'inertie polaire ? Quelle signification physique cette quantité a-t-elle ?
7. Dans quelles unités est-il mesuré ?
Exemple d'exécution
Pour une poutre donnée (Fig. 7.1), construire des diagrammes de couples, en utilisant une disposition rationnelle des poulies sur l'arbre pour réduire la valeur du couple maximum. Construire un diagramme de couples avec une disposition rationnelle des poulies. À partir de la condition de résistance, déterminez les diamètres des arbres pour les sections pleines et annulaires, en prenant c =. Comparez les résultats obtenus en fonction des zones transversales obtenues. [τ] = 35 MPa.
Solution
Section 2 (Fig.7.2b) :
Section 3 (Fig.7.3c) :

Figure 7.2

ABC
Figure 7.3
- Nous construisons un diagramme de couples. Nous mettons les valeurs de couple vers le bas de l'axe, car moments négatifs. La valeur maximale du couple sur l'arbre dans ce cas est de 1 000 Nm (Fig. 7.1).
- Choisissons une disposition rationnelle des poulies sur l'arbre. L'emplacement le plus approprié des poulies est tel que les valeurs de couple positives et négatives les plus grandes dans les sections soient aussi similaires que possible. Pour ces raisons, la poulie motrice, transmettant un couple de 1000 Nm, est placée plus près du centre de l'arbre, les poulies menées 1 et 2 sont placées à gauche de la poulie motrice avec un couple de 1000 Nm, la poulie 3 reste en le même endroit. Nous construisons un diagramme de couples pour la disposition de poulies sélectionnée (Fig. 7.3).
La valeur de couple maximale sur l'arbre pour la disposition de poulie sélectionnée est de 600 N*m.

Figure 7.4
Moment de torsion :
![]()
![]()
![]()
Nous déterminons les diamètres d'arbre par sections :
![]()
![]()
![]()
![]()
On arrondit les valeurs obtenues : , ,
- Nous déterminons les diamètres de l'arbre par sections, à condition que la section soit un anneau
Les moments de résistance restent les mêmes. Par condition
Moment de résistance polaire de l'anneau : ![]()
Formule pour déterminer le diamètre extérieur d'un arbre annulaire :

Le calcul peut être effectué à l'aide de la formule : 
Diamètres d'arbre sur toutes les sections :
![]()
![]()
![]()
Les diamètres extérieurs de l'arbre à section annulaire sont restés pratiquement inchangés.
Pour section annulaire : , ,
- Pour tirer une conclusion sur l'économie de métal lors du passage à une section annulaire, comparons les surfaces de section transversale (Fig. 7.4)
À condition que la section transversale soit un cercle (Fig. 7.4a)
Section ronde pleine :
![]()
![]()
![]()
À condition que la section transversale soit un anneau (Fig. 7.4b).
![]()
Section anneau :
![]()
![]()
![]()
Évaluation comparative des résultats :
![]()
Par conséquent, lors du passage d'une section circulaire à une section annulaire, l'économie de poids du métal sera de 1,3 fois.

Figure 7.4
Tableau 7.1
 |  |  |
 |  |  |
 |  |  |
 |
Tableau 7.2
| Option | Possibilités | |||
| une = b = s, m | Р1,kW | R2,kW | Р3,kW | |
| 1,1 | 2,1 | 2,6 | 3,1 | |
| 1,2 | 2,2 | 2,7 | 3,2 | |
| 1,3 | 2,3 | 2,8 | 3,3 | |
| 1,4 | 2,4 | 2,9 | 3,4 | |
| 1,5 | 2,5 | 3,0 | 3,5 | |
| 1,6 | 2,6 | 3,1 | 3,6 | |
| 1,7 | 2,7 | 3,2 | 3,7 | |
| 1,8 | 2,8 | 3,3 | 3,8 | |
| 1,9 | 2,9 | 3,4 | 3,9 | |
| 2,0 | 3,0 | 3,5 | 4,0 | |
| 1,1 | 3,1 | 3,4 | 4,1 | |
| 1,2 | 3,2 | 3,3 | 4,2 | |
| 1,3 | 3,3 | 3,2 | 4,3 | |
| 1,4 | 3,4 | 3,1 | 4,5 | |
| 1,5 | 3,5 | 2,8 | 2,9 | |
| 1,3 | 2,1 | 2,6 | 3,1 | |
| 1,4 | 2,2 | 2,7 | 3,2 | |
| 1,5 | 2,3 | 2,8 | 3,3 | |
| 1,6 | 2,4 | 2,9 | 3,4 | |
| 1,7 | 2,5 | 3,0 | 3,5 | |
| 1,8 | 2,6 | 3,1 | 3,6 | |
| 1,9 | 2,7 | 3,2 | 3,7 | |
| 2,0 | 2,8 | 3,3 | 3,8 | |
| 1,1 | 2,9 | 3,4 | 3,9 | |
| 1,2 | 3,0 | 3,5 | 4,0 | |
| 1,3 | 3,1 | 3,4 | 4,1 | |
| 1,4 | 3,2 | 3,3 | 4,2 | |
| 1,5 | 3,3 | 3,2 | 4,3 | |
| 1,4 | 3,4 | 3,1 | 4,5 | |
| 1,9 | 3,5 | 2,8 | 2,9 |
ANNEXE A
Torsion d’une tige de section circulaire – condition problématique
Quatre moments de torsion externes sont appliqués à un arbre en acier de section constante (Fig. 3.8) : kN m ; kNm; kNm; kNm. Longueurs des sections de tige : m ; m, m, m. Obligatoire : construire un diagramme des couples, déterminer le diamètre de l'arbre à kN/cm2 et construire un diagramme des angles de torsion des sections transversales de la tige.
Torsion d'une tige ronde - schéma de conception
 Riz. 3.8
Riz. 3.8
Solution au problème de torsion d'une tige ronde
Déterminer le couple réactif généré dans un joint rigide
Désignons le moment dans l'intégration et dirigeons-le, par exemple, dans le sens inverse des aiguilles d'une montre (en regardant vers l'axe z).
Écrivons l'équation d'équilibre de l'arbre. Dans ce cas, nous utiliserons la règle de signe suivante : les moments de torsion externes (moments actifs, ainsi que moment réactif dans le joint), faisant tourner l'arbre dans le sens inverse des aiguilles d'une montre (en le regardant vers l'axe z), sont considérés comme positifs.
Le signe plus dans l’expression que nous avons obtenue indique que nous avons deviné la direction du couple réactif apparaissant dans le joint.
Nous construisons un diagramme de couples
Rappelons que le couple interne apparaissant dans une certaine section transversale de la tige est égal à la somme algébrique des moments de torsion externes appliqués à l'une des parties considérées de la tige (c'est-à-dire agissant vers la gauche ou vers la droite de la coupe réalisée). Dans ce cas, le moment de torsion externe, qui fait tourner la partie de la tige considérée dans le sens inverse des aiguilles d'une montre (en regardant la section transversale), est inclus dans cette somme algébrique avec un signe « plus », et en cours de route – avec un « moins " signe.
En conséquence, le couple interne positif neutralisant les moments de torsion externes est dirigé dans le sens des aiguilles d'une montre (en regardant la section transversale) et le couple négatif dans le sens inverse des aiguilles d'une montre.
Nous divisons la longueur de la tige en quatre sections (Fig. 3.8, a). Les limites des sections sont les sections dans lesquelles des moments externes sont appliqués.
Nous réalisons une section à un endroit aléatoire dans chacune des quatre sections de la tige.
Section 1 – 1. Jetons mentalement (ou recouvrons d’un morceau de papier) le côté gauche de la tige. Pour équilibrer le moment de torsion kN m, un couple égal et de direction opposée doit apparaître dans la section transversale de la tige. Compte tenu de la règle de signalisation mentionnée ci-dessus
![]() kNm.
kNm.
Sections 2 – 2 et 3 – 3 :
Section 4 – 4. Pour déterminer le couple, dans la section 4 – 4, nous rejetons le côté droit de la tige. Alors
![]() kNm.
kNm.
Il est facile de vérifier que le résultat obtenu ne changera pas si l'on écarte maintenant non pas la partie droite, mais la partie gauche de la tige. On a
Pour construire un diagramme de couples, tracez une fine ligne le long de l'axe parallèle à l'axe de la tige z (Fig. 3.8, b). A partir de cet axe sont tracées les valeurs calculées des couples sur l'échelle choisie et tenant compte de leur signe. Au sein de chaque section de la tige, le couple est constant, nous semblons donc « ombrer » la section correspondante avec des lignes verticales. Rappelons que chaque segment des « hachures » (l'ordonnée du schéma) donne, sur l'échelle admise, la valeur du couple dans la section correspondante de la tige. Nous décrivons le diagramme obtenu avec un trait épais.
A noter qu'aux endroits où les moments de torsion externes sont appliqués sur le schéma, nous avons reçu une variation brusque du couple interne de la valeur du couple externe correspondant.
Déterminer le diamètre de l'arbre à partir de la condition de résistance
La condition de résistance à la torsion a la forme
 ,
,
Où ![]() – moment de résistance polaire (moment de résistance lors de la torsion).
– moment de résistance polaire (moment de résistance lors de la torsion).
La plus grande valeur absolue du couple se produit dans la deuxième section de l'arbre : ![]() kN cm
kN cm
Ensuite, le diamètre d'arbre requis est déterminé par la formule
 cm.
cm.
En arrondissant la valeur résultante à la valeur standard, nous prenons le diamètre de l'arbre égal à mm.
Nous déterminons les angles de torsion des sections transversales A, B, C, D et E et construisons un schéma des angles de torsion
Tout d’abord, nous calculons la rigidité en torsion de la tige, où G est le module de cisaillement, et ![]() – moment d'inertie polaire. On a
– moment d'inertie polaire. On a
Les angles de torsion dans les sections individuelles de la tige sont égaux :
 content;
content;
 content;
content;
 content;
content;
 content.
content.
L’angle de torsion dans l’encastrement est donc nul. Alors
Le diagramme des angles de torsion est présenté sur la Fig. 3.8, ch. Notez que sur la longueur de chaque section de l'arbre, l'angle de torsion change selon une loi linéaire.
Un exemple de problème de torsion d'une tige « ronde » pour solution indépendante
Conditions du problème de torsion d'une tige « ronde »
Une tige d'acier (module de cisaillement kN/cm2) de section circulaire, rigidement serrée à une extrémité, est tordue par quatre moments (Fig. 3.7).
Requis:
· construire un diagramme de couples ;
· à une contrainte de cisaillement admissible donnée kN/cm2, à partir de la condition de résistance, déterminer le diamètre de l'arbre en l'arrondissant à la plus proche des valeurs suivantes 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 millimètres ;
· construire un diagramme des angles de torsion des sections transversales de la tige.
Variantes de schémas de calcul pour le problème de torsion d'une tige ronde pour une solution indépendante

Un exemple de problème de torsion d'une tige ronde - conditions initiales pour une solution indépendante
| Numéro de régime | ||||||||
|
Sélectionnez les dimensions de la section transversale de l'arbre (Fig. 1) en fonction des conditions de résistance. Dans les sections de la section 1 à la section 3 et de la section 5 à la section 6, le diamètre extérieur de l'arbre, pour des raisons de conception, doit avoir la même taille.
Dans la section allant de la section 1 à la section 2, l'arbre présente une section annulaire avec n = d B /d = 0,4. Dans les sections de la section 3 à la section 5, l'arbre est sélectionné uniquement en fonction des conditions de résistance.
M = 1 kN∙m, [τ ] = 80 MPa.
Solution
Nous divisons l'arbre en sections de puissance et construisons un diagramme de couple (Fig. 1, b).
Déterminez les diamètres des arbres. Dans les sections I, II et V, le diamètre extérieur de l'arbre est le même. Pour eux, il n'est pas possible de prédéfinir la section avec la valeur de contrainte tangentielle la plus élevée, car les différentes sections ont différents types de section : la section I est circulaire, les sections II et V sont rondes pleines.
Il est nécessaire de déterminer séparément, en fonction de la condition de résistance, les diamètres pour chaque type de section pour la section de puissance la plus chargée (c'est-à-dire celle sur laquelle agit la valeur absolue maximale du couple). On retiendra finalement le plus grand diamètre obtenu.
Pour une section avec une section en anneau :
Pour un arbre de section pleine

Enfin, on accepte la plus grande valeur du diamètre résultant, arrondie à la valeur entière la plus proche :
d 1 = d 2 = d 5 = 61 mm ;
d B1 = n∙d 1 = 0,4∙61 = 24,4 mm.
La tension la plus élevée agissant dans ces zones est :
Diamètre de l'arbre en section III (M K3 = 5M = 5 kNm).
Tâche 4
Pour arbre en acier de section constante
1. Déterminer la valeur des moments M 1, M 2, M 3, M 4 ;
2. Construire un diagramme de couples ;
3. Déterminez le diamètre de l'arbre à partir de calculs de résistance et de rigidité, en prenant la section transversale de l'arbre - un cercle
P1 = 50 kW
P3 = 15 kW
P4 = 25 kW
w = 18 rad/sec
w = n = = 30*18/3,14 = 172 tr/min
[ts 0 ] =0,02 rad/m - angle de torsion
G = 8*10 4 MPa


On détermine les moments extérieurs :
M1 = 9 550 = 9 550 = 2 776 Nm = 2,8 kNm ;
M 3 = 9 550 = 9 550 = 832,8 Nm = 0,83 kNm ;
M 4 = 9 550 = 9 550 = 1 388 Nm = 1,4 kNm ;
Écrivons l'équation statique :
UM = M1 + M3 - M2 + M4 = 0
Et à partir de là on trouve la valeur du moment M 2 :
M 2 = M 3 + M 1 + M 4 = 832,8 +2776 +1388 = 4996,8 Nm = 5 kNm ;
Tout d'abord, nous construisons un diagramme de couple. Les valeurs de couple pour les sections sont les suivantes :
T 1 = -M 1 = -2,8 kNm ;
T 2 = -M 1 - M 3 = -2,8 - 0,83 = - 3,63 kNm ;
T 3 = -M 1 - M 3 + M 2 = -3,63 + 5 = 1,37 kNm.
Nous construisons des schémas :
Le puits est divisé en trois sections I, II, III.

On retrouve le moment polaire de résistance de l'arbre requis par la condition de résistance :
W p = = = 121 10 -6 m 3 = 121 cm 3
Le diamètre de l'arbre plein est déterminé à l'aide de la formule :
W p 0,2d c 3 = 121 cm 3,
d c 3 = = 8,46 cm 9 cm = 90 mm.
Ensuite, les diamètres sont calculés pour les sections d'arbre en fonction de la condition de rigidité, c'est-à-dire en utilisant une formule

d geste1 = = 0,1 m = 100 mm

d geste2 = = 0,1068 m = 107 mm

d geste1 = = 0,0837 m = 84 mm
Les valeurs de diamètre les plus grandes calculées à partir de la condition de rigidité doivent être sélectionnées comme valeurs finales. Ainsi, la taille finale du diamètre de l'arbre est : d 1 = 107 mm.
De la gamme standard : d 1 = 120 mm
Tâche 5
Une poulie et une roue sont montées rigidement sur l'arbre,
Déterminer les forces F 2 .F 2r = 0,4 F 1 si la valeur de la force F 1 est donnée

Imaginons un système physique :

Nous résolvons le problème dans l’ordre suivant :
1. Nous représentons sur la figure le corps dont l'équilibre est considéré, avec des forces actives et réactives agissant sur lui et sélectionnons un système d'axes de coordonnées ;
2. A partir de la condition d'équilibre d'un corps ayant un axe fixe, on détermine les valeurs des forces F 2, F r2 ;
3. composer six équations d'équilibre ;
4. résoudre des équations et déterminer les réactions de support ;
5. Vérifiez l'exactitude de la solution au problème.
1. Nous représentons l'arbre avec toutes les forces agissant sur lui, ainsi que les axes de coordonnées

Considérons un système de forces agissant dans le système
Déterminer les composantes de la charge côté poulie
P 1 = (2F 1 + F 1) = 3 F 1 = 3*280 = 840 N = 0,84 kN

2. Déterminez F2 et Fr2. De la condition d'équilibre d'un corps ayant un axe fixe :
F 2 = = = 507,5 H
F r2 = 0,4F2 = 0,4*507,5 = 203 H
3. Nous composons six équations d'équilibre :
AA = -P 1 - F 2 + A y + B y = 0 (1)
УX = -F 2r + A x + B x = 0 (2)
UM yC = -P 1 * 32 + A y * 20 - B y * 10 = 0 (3)
UM yB = - P 1 * 42 + A y * 30 - F 2 * 10 = 0 (4)
UM xC = A x * 20 - V x * 10 = 0 (5)
UM xB = A x * 30 + F 2r * 10 = 0 (6)
Considérez les équations (3) et (4)
840 * 32 + A y * 20 - B y * 10 = 0
840 * 42 + A y * 30 - 507,5 *10 = 0
De la dernière équation :
UNE y = 40355/30 = 1345 N
De la première équation :
26880 + 26900 = 10*V y ? V y = 20/10 = 2 N
Considérez les équations (5) et (6)
A x * 20 - B x * 10 = 0
Un x * 30 + 203 * 10 = 0
D'après la dernière équation A x = 2030/30 = 67,7 N
D'après la première équation : 1353,3 = 10*V y ? V y = 1353/10 = 135,3 N
Nous vérifierons à l'aide des équations (1) et (2) :
AA = -840 - 507,5 + 1345 + 2 = 0
УX = -203 + 67,7 + 135,3 = 0
Les calculs ont été effectués correctement. Les réactions finales des supports A et B sont :
A = = = 1346,7N




B = = = 135,3 N