Finden Sie den Durchmesser im Drehmoment. Berechnungen der Festigkeit und Torsionssteifigkeit
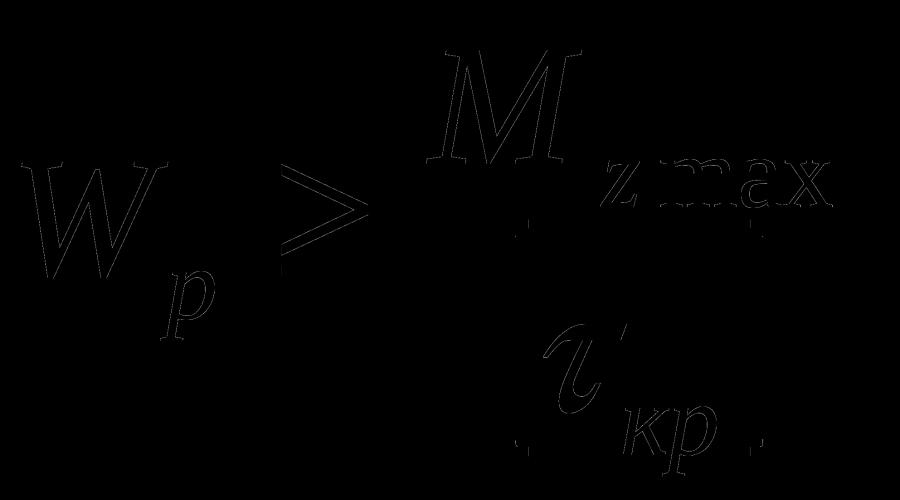
Lesen Sie auch
DREHUNG
Reihenfolge der Lösung des Problems
1. Bestimmen Sie die äußeren Torsionsmomente mit der Formel
M=P/ω
Wo R - Leistung,
ω - Winkelgeschwindigkeit.
2. Da bei gleichmäßiger Drehung der Welle die algebraische Summe der auf sie ausgeübten äußeren Torsionsmomente (Rotationsmomente) gleich Null ist, bestimmen Sie das Ausgleichsmoment anhand der Gleichgewichtsgleichung
∑ M i z = 0
3. Erstellen Sie mithilfe der Abschnittsmethode ein Diagramm der Drehmomente entlang der Länge der Welle.
4. Bestimmen Sie für den Abschnitt der Welle, in dem das größte Drehmoment auftritt, den Durchmesser der Welle mit rundem oder ringförmigem Querschnitt anhand der Festigkeits- und Steifigkeitsbedingungen. Nehmen Sie für den ringförmigen Abschnitt der Welle das Durchmesserverhältnis
Wo D Ö- Innendurchmesser des Rings;
D - Außendurchmesser des Rings.
Aus der Festigkeitsbedingung:
Aus der Steifigkeitsbedingung:


Wo M zmax- maximales Drehmoment;
W P - polares Torsionsmoment;
[τ cr] - zulässige Scherspannung
Wo J P - polares Trägheitsmoment des Abschnitts;
G - Schubelastizitätsmodul;
[φ Ö] - zulässiger Verdrehungswinkel des Abschnitts
Wellenquerschnitt - Kreis


Erforderlicher Schaftdurchmesser für Festigkeit:
Erforderlicher Wellendurchmesser für Steifigkeit:


Wellenabschnitt - Ring


Erforderlicher Festigkeitsaußenringdurchmesser:
Erforderlicher Steifigkeitsaußendurchmesser des Rings:


Beispiel 1 . Für eine Stahlwelle (Abb. 1) mit konstantem Querschnitt über die Länge ist Folgendes erforderlich: 1) Bestimmen Sie die Werte der Momente M 2 Und M 3 , entsprechend den übertragenen Leistungen R 2 Und R 3 sowie das Ausgleichsmoment M 1 ; 2) Erstellen Sie ein Diagramm der Drehmomente; 3) Bestimmen Sie den erforderlichen Wellendurchmesser anhand von Festigkeits- und Steifigkeitsberechnungen, je nach Option (A) (B) - C =d 0 / d=0,8.
Akzeptieren: [ τ cr ] = 30 MPa ; [ φ 0 ] = 0,02 rad/m; R 2 = 52 kW; R 3 = 50 kW; ω = 20 rad/s; G = 8 10 4 MPa

Reis. 1 - Problemdiagramm
Lösung:
1. Bestimmen Sie äußere Verdrehmomente:
M 2 = P 2 / ω = 52 10 3 / 20 = 2600 N m
M 3 = P 3 / ω = 50 10 3 / 20 = 2500 N m
2. Bestimmen Sie das Ausgleichsmoment M 1 :
∑ M i z = 0; M 1 – M 2 – M 3 =0
M 1 = M 2 + M 3 = 5100 Nm
3. Bestimmen Sie das Drehmoment nach Wellenabschnitten:
M z ICH= M 1 = 5100 N m
M z II= M 1 – M 2 = 5100 – 2600 = 2500 N·m
Wir erstellen ein Drehmomentdiagramm Mz(Abb. 2).

Reis. 2 - Drehmomentdiagramm
4. Wir bestimmen den Durchmesser der Welle anhand der Festigkeits- und SteifigkeitsbedingungenM z max = 5100 N M(Abb. 2).
a) Schaftabschnitt – Kreis.
Aus der Festigkeitsbedingung:
Wir akzeptieren D = 96 mm
Aus der Steifigkeitsbedingung:
Wir akzeptieren D = 76 mm
Der erforderliche Durchmesser erwies sich aufgrund der Festigkeit als größer, daher gehen wir davon aus, dass der endgültige Durchmesser d = 96 mm beträgt.
b) Der Querschnitt der Welle ist ein Ring.
Aus der Festigkeitsbedingung:
Wir akzeptieren D = 114 mm
Aus der Steifigkeitsbedingung:
Wir akzeptieren D = 86 mm
Die erforderlichen Durchmesser ergeben sich abschließend aus Festigkeitsberechnungen:
Ringaußendurchmesser D = 114 mm
Innendurchmesser des Pfahls tsa D Ö = 0,8 D = 0,8 114 = 91,2 mm. Wir akzeptieren D Ö =92 mm .
Aufgabe 1. Für eine Stahlwelle (Abb. 3) mit konstantem Querschnitt ist Folgendes erforderlich: 1) Bestimmen Sie die Werte der Momente M 1 , M 2 , M 3 Und M 4 ; 2) Erstellen Sie ein Diagramm der Drehmomente; 3) Bestimmen Sie den Durchmesser der Welle anhand von Festigkeits- und Steifigkeitsberechnungen, je nach Option (A) der Querschnitt der Welle ist ein Kreis; je nach Option (B)- Querschnitt einer Welle – ein Ring mit einem Durchmesserverhältnis C =d 0 /d=0,7. Getriebeleistung übernehmen R 2 = 0,5R 1 ; R 3 = 0,3Р 1 ; R 4 = 0,2Р 1 .
Akzeptieren: [ τ cr ] = 30 MPa ; [ φ 0 ] = 0,02 rad/m; G = 8 10 4 MPa
Runden Sie den endgültigen Durchmesserwert auf die nächste gerade Zahl (oder die Zahl, die auf fünf endet).
Entnehmen Sie die Daten für Ihre Option der Tabelle 1
Notiz. Runden Sie den resultierenden berechneten Durchmesserwert (in mm) auf die nächstgrößere Zahl mit der Endung 0, 2, 5, 8.
Tabelle 1 – Ausgangsdaten
Schemanummer in Abbildung 3.2.5
P 1
Optionen
rad/s
kW

Reis. 3 - Problemdiagramm
Übung
Bestimmen Sie für eine Stahlwelle mit kreisförmigem Querschnitt die Werte der äußeren Momente, die den übertragenen Kräften und dem ausgeglichenen Moment entsprechen (Tabelle 7.1 und Tabelle 7.2).
Erstellen Sie ein Diagramm der Drehmomente entlang der Länge der Welle.
Bestimmen Sie die Wellendurchmesser nach Querschnitt anhand von Festigkeits- und Steifigkeitsberechnungen. Runden Sie das resultierende größere Ergebnis auf die nächste gerade Zahl oder enden Sie auf 5.
Berücksichtigen Sie bei der Berechnung folgende Daten: Die Welle dreht sich mit einer Winkelgeschwindigkeit von 25 rad/s; Schaftmaterial - Stahl, zulässige Torsionsspannung 30 MPa, Schubelastizitätsmodul 8 · 10 4 MPa; zulässiger Verdrehwinkel = 0,02 rad/m.
Führen Sie Berechnungen für eine Welle mit ringförmigem Querschnitt durch Mit= 0,9. Ziehen Sie durch den Vergleich der Querschnittsflächen Rückschlüsse auf die Zweckmäßigkeit, einen Schaft mit rundem oder ringförmigem Querschnitt herzustellen.
Ziel der Arbeit - Sie lernen, Konstruktions- und Nachweisberechnungen für Rundträger für statisch bestimmte Systeme durchzuführen und die Steifigkeit zu prüfen.
Theoretischer Hintergrund
Torsion ist eine Belastung, bei der im Querschnitt des Balkens nur ein interner Kraftfaktor auftritt – das Drehmoment. Äußere Lasten sind ebenfalls zwei entgegengesetzt gerichtete Kräftepaare.
Verteilung der Tangentialspannungen über einen Abschnitt während der Torsion (Abb. 7.1)
Schubspannung an einem Punkt A:

Abb.7.1
 (7.1)
(7.1)
Wo ist der Abstand vom Punkt? A Vor
Mitte des Abschnitts.
Zustand der Torsionsfestigkeit
![]() ;
; ![]() (Kreis), (7.2)
(Kreis), (7.2)
![]() (Ring), (7.3)
(Ring), (7.3)
wobei M k das Drehmoment im Abschnitt ist, N-m, N-mm;
Wp- Widerstandsmoment bei Torsion, m 3, mm 3;
[t k] – zulässige Torsionsspannung, N/m 2, N/mm 2.
Bemessungsberechnung, Ermittlung der Querschnittsmaße
 (7.4)
(7.4)
Wo D- Außendurchmesser des kreisförmigen Abschnitts;
d B n– Innendurchmesser des ringförmigen Abschnitts; c = d BK /d.
Bestimmen der sinnvollen Lage der Radwelle
Eine rationelle Anordnung der Räder ist eine Anordnung, bei der der maximale Wert des Drehmoments auf der Welle so klein wie möglich ist.
Zustand der Torsionssteifigkeit
; G ≈ 0,4E(7.5)
Wo G- Schubelastizitätsmodul, N/m 2, N/mm 2;
E- Zugelastizitätsmodul, N/m 2, N/mm 2.
[φо] – zulässiger Verdrehungswinkel, [φо] = 0,54-1 Grad/m;
Jp- polares Trägheitsmoment im Abschnitt, m 4, mm 4.
 (7.6) (7.6)
|
Konstruktionsberechnung, Bestimmung des Außendurchmessers des Abschnitts
Arbeitsauftrag
1. Erstellen Sie ein Diagramm der Drehmomente über die Länge der Welle für den in der Aufgabe vorgeschlagenen Stromkreis.
2. Wählen Sie eine rationelle Anordnung der Räder auf der Welle und führen Sie weitere Berechnungen für eine Welle mit rational angeordneten Riemenscheiben durch.
3. Bestimmen Sie die erforderlichen Durchmesser einer kreisförmigen Welle anhand von Festigkeit und Steifigkeit und wählen Sie den größten der erhaltenen Werte aus, indem Sie den Durchmesser runden.
4. Vergleichen Sie die Metallkosten für kreisförmige und ringförmige Abschnitte. Der Vergleich erfolgt anhand der Querschnittsflächen der Wellen.
Kontrollfragen
1. Welche Verformungen treten bei der Torsion auf?
2. Welche Hypothesen gelten für Torsionsverformungen?
3. Ändern sich Länge und Durchmesser des Schafts nach dem Verdrehen?
4. Welche inneren Kraftfaktoren entstehen bei der Torsion?
5. Wie ist die sinnvolle Anordnung der Ohren am Schaft?
6. Was ist das polare Trägheitsmoment? Welche physikalische Bedeutung hat diese Größe?
7. In welchen Einheiten wird es gemessen?
Ausführungsbeispiel
Erstellen Sie für einen gegebenen Balken (Abb. 7.1) Drehmomentdiagramme und verwenden Sie dabei eine sinnvolle Anordnung der Riemenscheiben auf der Welle, um den Wert des maximalen Drehmoments zu reduzieren. Erstellen Sie ein Drehmomentdiagramm mit einer rationalen Anordnung der Riemenscheiben. Bestimmen Sie aus der Festigkeitsbedingung die Durchmesser der Wellen für Voll- und Ringquerschnitte mit c =. Vergleichen Sie die erhaltenen Ergebnisse anhand der erhaltenen Querschnittsflächen. [τ] = 35 MPa.
Lösung
Abschnitt 2 (Abb.7.2b):
Abschnitt 3 (Abb.7.3c):

Abb.7.2

A B C
Abb.7.3
- Wir erstellen ein Drehmomentdiagramm. Wir tragen die Drehmomentwerte von der Achse ab, weil negative Momente. Das maximale Drehmoment an der Welle beträgt in diesem Fall 1000 Nm (Abb. 7.1).
- Wählen wir eine rationelle Anordnung der Riemenscheiben auf der Welle. Die am besten geeignete Platzierung der Riemenscheiben ist so, dass die größten positiven und negativen Drehmomentwerte in den Abschnitten möglichst ähnlich sind. Aus diesen Gründen wird die Antriebsscheibe, die ein Drehmoment von 1000 Nm überträgt, näher an der Mitte der Welle platziert, die Abtriebsscheiben 1 und 2 werden links von der Antriebsscheibe mit einem Drehmoment von 1000 Nm platziert, Riemenscheibe 3 bleibt drin der gleiche Platz. Wir erstellen ein Diagramm der Drehmomente für die gewählte Anordnung der Riemenscheiben (Abb. 7.3).
Das maximale Drehmoment an der Welle beträgt bei der gewählten Riemenscheibenanordnung 600 N*m.

Abb.7.4
Torsionsmoment:
![]()
![]()
![]()
Wir ermitteln die Wellendurchmesser nach Abschnitten:
![]()
![]()
![]()
![]()
Wir runden die erhaltenen Werte: , ,
- Wir bestimmen die Durchmesser der Welle abschnittsweise, sofern es sich bei dem Abschnitt um einen Ring handelt
Die Widerstandsmomente bleiben gleich. Nach Bedingung
Polares Widerstandsmoment des Rings: ![]()
Formel zur Bestimmung des Außendurchmessers einer Ringwelle:

Die Berechnung kann mit der Formel erfolgen: 
Wellendurchmesser über die Abschnitte:
![]()
![]()
![]()
Die Außendurchmesser der Ringwelle sind nahezu unverändert geblieben.
Für ringförmigen Abschnitt: , ,
- Um eine Schlussfolgerung über die Metalleinsparungen bei der Umstellung auf einen ringförmigen Abschnitt zu ziehen, vergleichen wir die Querschnittsflächen (Abb. 7.4).
Vorausgesetzt, der Querschnitt ist ein Kreis (Abb. 7.4a)
Massiver runder Abschnitt:
![]()
![]()
![]()
Vorausgesetzt, der Querschnitt ist ein Ring, (Abb. 7.4b)
![]()
Ringabschnitt:
![]()
![]()
![]()
Vergleichende Bewertung der Ergebnisse:
![]()
Beim Wechsel von einem kreisförmigen zu einem ringförmigen Abschnitt beträgt die Gewichtseinsparung an Metall folglich das 1,3-fache.

Abb.7.4
Tabelle 7.1
 |  |  |
 |  |  |
 |  |  |
 |
Tabelle 7.2
| Möglichkeit | Optionen | |||
| a = b = s, m | Р1,kW | Р2,kW | Р3,kW | |
| 1,1 | 2,1 | 2,6 | 3,1 | |
| 1,2 | 2,2 | 2,7 | 3,2 | |
| 1,3 | 2,3 | 2,8 | 3,3 | |
| 1,4 | 2,4 | 2,9 | 3,4 | |
| 1,5 | 2,5 | 3,0 | 3,5 | |
| 1,6 | 2,6 | 3,1 | 3,6 | |
| 1,7 | 2,7 | 3,2 | 3,7 | |
| 1,8 | 2,8 | 3,3 | 3,8 | |
| 1,9 | 2,9 | 3,4 | 3,9 | |
| 2,0 | 3,0 | 3,5 | 4,0 | |
| 1,1 | 3,1 | 3,4 | 4,1 | |
| 1,2 | 3,2 | 3,3 | 4,2 | |
| 1,3 | 3,3 | 3,2 | 4,3 | |
| 1,4 | 3,4 | 3,1 | 4,5 | |
| 1,5 | 3,5 | 2,8 | 2,9 | |
| 1,3 | 2,1 | 2,6 | 3,1 | |
| 1,4 | 2,2 | 2,7 | 3,2 | |
| 1,5 | 2,3 | 2,8 | 3,3 | |
| 1,6 | 2,4 | 2,9 | 3,4 | |
| 1,7 | 2,5 | 3,0 | 3,5 | |
| 1,8 | 2,6 | 3,1 | 3,6 | |
| 1,9 | 2,7 | 3,2 | 3,7 | |
| 2,0 | 2,8 | 3,3 | 3,8 | |
| 1,1 | 2,9 | 3,4 | 3,9 | |
| 1,2 | 3,0 | 3,5 | 4,0 | |
| 1,3 | 3,1 | 3,4 | 4,1 | |
| 1,4 | 3,2 | 3,3 | 4,2 | |
| 1,5 | 3,3 | 3,2 | 4,3 | |
| 1,4 | 3,4 | 3,1 | 4,5 | |
| 1,9 | 3,5 | 2,8 | 2,9 |
ANHANG A
Torsion eines Stabes mit kreisförmigem Querschnitt – Problemzustand
Auf eine Stahlwelle mit konstantem Querschnitt wirken vier äußere Torsionsmomente (Abb. 3.8): kN·m; kN·m; kN·m; kNm. Längen der Stababschnitte: m; m, m, m. Erforderlich: Erstellen Sie ein Diagramm der Drehmomente, bestimmen Sie den Durchmesser der Welle bei kN/cm2 und erstellen Sie ein Diagramm der Verdrehungswinkel der Stabquerschnitte.
Torsion eines Rundstabes - Konstruktionsdiagramm
 Reis. 3.8
Reis. 3.8
Lösung des Problems der Torsion eines Rundstabes
Bestimmen Sie das Reaktionsmoment, das in einer starren Dichtung auftritt
Bestimmen wir den Moment in der Einbettung und richten ihn beispielsweise gegen den Uhrzeigersinn (bei Blick auf die Z-Achse).
Schreiben wir die Gleichgewichtsgleichung für die Welle auf. In diesem Fall verwenden wir die folgende Vorzeichenregel: Äußere Drehmomente (aktive Momente sowie Reaktionsmoment in der Dichtung), die die Welle gegen den Uhrzeigersinn drehen (bei Betrachtung in Richtung der z-Achse), werden als positiv betrachtet.
Das Pluszeichen in dem von uns erhaltenen Ausdruck zeigt an, dass wir die Richtung des in der Dichtung auftretenden Reaktionsdrehmoments erraten haben.
Wir erstellen ein Drehmomentdiagramm
Erinnern wir uns daran, dass das in einem bestimmten Querschnitt der Stange auftretende innere Drehmoment gleich der algebraischen Summe der äußeren Drehmomente ist, die auf einen der betrachteten Teile der Stange wirken (d. h. nach links oder rechts wirkend). des erstellten Abschnitts). In diesem Fall geht das äußere Drehmoment, das den betrachteten Teil des Stabes bei Betrachtung des Querschnitts gegen den Uhrzeigersinn dreht, mit einem „Plus“-Zeichen in diese algebraische Summe ein und nebenbei – mit einem „Minus“. " Zeichen.
Dementsprechend ist das positive innere Drehmoment, das den äußeren Verdrehmomenten entgegenwirkt, im Uhrzeigersinn (bei Betrachtung des Querschnitts) und das negative gegen den Uhrzeigersinn gerichtet.
Wir teilen die Länge des Stabes in vier Abschnitte (Abb. 3.8, a). Die Grenzen der Abschnitte sind diejenigen Abschnitte, in denen äußere Momente wirken.
Wir machen einen Abschnitt an einer zufälligen Stelle in jedem der vier Abschnitte der Stange.
Abschnitt 1 – 1. Lassen Sie uns die linke Seite der Stange im Geiste wegwerfen (oder mit einem Stück Papier abdecken). Um das Verdrehmoment kN·m auszugleichen, muss im Stabquerschnitt ein gleiches und entgegengesetzt gerichtetes Drehmoment entstehen. Unter Berücksichtigung der oben genannten Vorzeichenregel
![]() kNm.
kNm.
Abschnitte 2 – 2 und 3 – 3:
Abschnitt 4 – 4. Um das Drehmoment zu bestimmen, werfen wir in Abschnitt 4 – 4 die rechte Seite der Stange weg. Dann
![]() kNm.
kNm.
Es ist leicht zu überprüfen, dass sich das erhaltene Ergebnis nicht ändert, wenn wir jetzt nicht den rechten, sondern den linken Teil der Stange wegwerfen. Wir bekommen
Um ein Drehmomentdiagramm zu erstellen, zeichnen Sie eine dünne Linie entlang der Achse parallel zur Stabachse z (Abb. 3.8, b). Auf dieser Achse werden die berechneten Werte der Drehmomente im gewählten Maßstab und unter Berücksichtigung ihres Vorzeichens aufgetragen. In jedem Abschnitt der Stange ist das Drehmoment konstant, sodass wir den entsprechenden Abschnitt scheinbar mit vertikalen Linien „schattieren“. Erinnern wir uns daran, dass jedes Segment der „Schraffur“ (die Ordinate des Diagramms) im akzeptierten Maßstab den Wert des Drehmoments im entsprechenden Querschnitt der Stange angibt. Das resultierende Diagramm umreißen wir mit einer dicken Linie.
Beachten Sie, dass wir an den Stellen, an denen im Diagramm äußere Drehmomente wirken, eine abrupte Änderung des inneren Drehmoments um den Wert des entsprechenden äußeren Drehmoments erhalten haben.
Bestimmen Sie den Schaftdurchmesser aus dem Festigkeitszustand
Die Torsionsfestigkeitsbedingung hat die Form
 ,
,
Wo ![]() – polares Widerstandsmoment (Widerstandsmoment bei Torsion).
– polares Widerstandsmoment (Widerstandsmoment bei Torsion).
Der größte absolute Drehmomentwert tritt im zweiten Abschnitt der Welle auf: ![]() kNcm
kNcm
Anschließend wird der benötigte Wellendurchmesser durch die Formel ermittelt
 cm.
cm.
Wenn wir den resultierenden Wert auf den Standardwert runden, nehmen wir an, dass der Wellendurchmesser mm ist.
Wir bestimmen die Verdrehungswinkel der Querschnitte A, B, C, D und E und erstellen ein Diagramm der Verdrehungswinkel
Zuerst berechnen wir die Torsionssteifigkeit des Stabes, wobei G der Schubmodul ist und ![]() – polares Trägheitsmoment. Wir bekommen
– polares Trägheitsmoment. Wir bekommen
Die Verdrehungswinkel in den einzelnen Abschnitten der Stange sind gleich:
 froh;
froh;
 froh;
froh;
 froh;
froh;
 froh.
froh.
Der Verdrehungswinkel in der Einbettung ist also Null. Dann
Das Diagramm der Verdrehungswinkel ist in Abb. dargestellt. 3,8, c. Beachten Sie, dass sich der Verdrehungswinkel innerhalb der Länge jedes Abschnitts der Welle nach einem linearen Gesetz ändert.
Ein Beispiel für ein Problem zur Torsion eines „runden“ Stabes zur unabhängigen Lösung
Bedingungen für das Problem der Torsion eines „runden“ Stabes
Ein an einem Ende starr eingespannter Stahlstab (Schubmodul kN/cm2) mit kreisförmigem Querschnitt wird um vier Momente verdreht (Abb. 3.7).
Erforderlich:
· Erstellen Sie ein Diagramm der Drehmomente;
· Bestimmen Sie bei einer gegebenen zulässigen Scherspannung kN/cm2 aus der Festigkeitsbedingung den Durchmesser der Welle und runden Sie ihn auf den nächsten der folgenden Werte ab: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 200 mm;
· Erstellen Sie ein Diagramm der Verdrehungswinkel der Stabquerschnitte.
Varianten von Berechnungsschemata für das Problem der Torsion eines Rundstabes zur eigenständigen Lösung

Ein Beispiel für ein Problem zur Torsion eines Rundstabes – Ausgangsbedingungen für eine unabhängige Lösung
| Schemanummer | ||||||||
|
Wählen Sie die Abmessungen des Schaftquerschnitts (Abb. 1) entsprechend dem Festigkeitszustand. In den Abschnitten von Abschnitt 1 bis Abschnitt 3 und von Abschnitt 5 bis Abschnitt 6 muss der Außendurchmesser der Welle aus konstruktiven Gründen gleich groß sein.
Im Abschnitt von Abschnitt 1 bis Abschnitt 2 weist die Welle einen ringförmigen Querschnitt mit n=d B /d=0,4 auf. In den Abschnitten von Abschnitt 3 bis Abschnitt 5 wird der Schaft nur nach Festigkeitsverhältnissen ausgewählt.
M = 1 kN∙m, [τ] = 80 MPa.
Lösung
Wir unterteilen die Welle in Leistungsabschnitte und erstellen ein Drehmomentdiagramm (Abb. 1, b).
Bestimmen Sie die Wellendurchmesser. In den Abschnitten I, II und V ist der Außendurchmesser der Welle gleich. Für sie ist es nicht möglich, den Abschnitt mit dem höchsten Tangentialspannungswert vorab festzulegen, da verschiedene Abschnitte unterschiedliche Querschnittstypen haben: Abschnitt I ist kreisförmig, Abschnitt II und V sind massiv rund.
Es ist erforderlich, die Durchmesser je nach Festigkeitszustand für jeden Querschnittstyp für den am stärksten belasteten Leistungsteil (d. h. denjenigen, auf den der maximale Absolutwert des Drehmoments wirkt) separat zu bestimmen. Wir akzeptieren schließlich den größten erhaltenen Durchmesser.
Für einen Abschnitt mit Ringquerschnitt:
Für eine Welle mit Vollquerschnitt

Wir akzeptieren schließlich den größten Wert des resultierenden Durchmessers, aufgerundet auf den nächsten ganzen Wert:
d 1 = d 2 = d 5 = 61 mm;
d B1 = n∙d 1 = 0,4∙61 = 24,4 mm.
Die höchste in diesen Bereichen wirkende Spannung beträgt:
Wellendurchmesser im Abschnitt III (M K3 = 5M = 5 kNm).
Aufgabe 4
Für Stahlwelle mit konstantem Querschnitt
1. Bestimmen Sie den Wert der Momente M 1, M 2, M 3, M 4;
2. Erstellen Sie ein Drehmomentdiagramm.
3. Bestimmen Sie den Durchmesser der Welle anhand von Festigkeits- und Steifigkeitsberechnungen, indem Sie den Querschnitt der Welle – einen Kreis – heranziehen
P 1 = 50 kW
P 3 = 15 kW
P 4 = 25 kW
w = 18 rad/sek
w = n = = 30*18/3,14 = 172 U/min
[ts 0 ] =0,02 rad/m – Verdrehungswinkel
G = 8*10 4 MPa


Wir bestimmen die äußeren Momente:
M 1 = 9550 = 9550 = 2776 Nm = 2,8 kNm;
M 3 = 9550 = 9550 = 832,8 Nm = 0,83 kNm;
M 4 = 9550 = 9550 = 1388 Nm = 1,4 kNm;
Schreiben wir die statische Gleichung:
UM = M 1 + M 3 – M 2 + M 4 = 0
Und daraus ermitteln wir den Wert des Moments M 2:
M 2 = M 3 + M 1 + M 4 = 832,8 +2776 +1388 = 4996,8 Nm = 5 kNm;
Zunächst erstellen wir ein Drehmomentdiagramm. Die Drehmomentwerte für die Abschnitte sind wie folgt:
T 1 = -M 1 = -2,8 kNm;
T 2 = -M 1 - M 3 = -2,8 - 0,83 = - 3,63 kNm;
T 3 = -M 1 - M 3 + M 2 = -3,63 + 5 = 1,37 kNm.
Wir erstellen Diagramme:
Der Schacht ist in drei Abschnitte I, II, III unterteilt.

Wir ermitteln das polare Widerstandsmoment der Welle, das für die Festigkeitsbedingung erforderlich ist:
W p = = = 121 10 -6 m 3 = 121 cm 3
Der Durchmesser der Vollwelle wird nach folgender Formel ermittelt:
W p 0,2d c 3 = 121 cm 3,
d c 3 = = 8,46 cm 9 cm = 90 mm.
Anschließend werden die Durchmesser für die Wellenabschnitte anhand der Steifigkeitsbedingung berechnet, d. h. Formel verwenden

d Geste1 = = 0,1 m = 100 mm

d Geste2 = = 0,1068 m = 107 mm

d Geste1 = = 0,0837 m = 84 mm
Als endgültige Werte sollten die größten aus der Steifigkeitsbedingung berechneten Durchmesserwerte ausgewählt werden. Somit beträgt die endgültige Größe des Wellendurchmessers: d 1 = 107 mm.
Aus dem Standardbereich: d 1 = 120 mm
Aufgabe 5
Auf der Welle sind eine Riemenscheibe und ein Rad fest montiert,
Bestimmen Sie die Kräfte F 2 .F 2r = 0,4 F 1, wenn der Wert der Kraft F 1 gegeben ist

Stellen wir uns ein physikalisches System vor:

Wir lösen das Problem in der folgenden Reihenfolge:
1. Wir stellen in der Abbildung den Körper dar, dessen Gleichgewicht betrachtet wird, mit den auf ihn einwirkenden aktiven und reaktiven Kräften und wählen ein System von Koordinatenachsen aus;
2. Aus dem Gleichgewichtszustand eines Körpers mit fester Achse bestimmen wir die Werte der Kräfte F 2, F r2;
3. sechs Gleichgewichtsgleichungen aufstellen;
4. Gleichungen lösen und Stützreaktionen bestimmen;
5. Überprüfen Sie die Richtigkeit der Lösung des Problems.
1. Wir stellen die Welle mit allen auf sie einwirkenden Kräften sowie den Koordinatenachsen dar

Betrachten wir ein System von Kräften, die im System wirken
Bestimmen Sie die Komponenten der Last auf der Riemenscheibenseite
P 1 = (2F 1 + F 1) = 3 F 1 = 3*280 = 840 N = 0,84 kN

2. Bestimmen Sie F2 und Fr2. Aus dem Gleichgewichtszustand eines Körpers mit fester Achse:
F 2 = = = 507,5 H
F r2 = 0,4F 2 = 0,4*507,5 = 203 H
3. Wir stellen sechs Gleichgewichtsgleichungen auf:
YY = -P 1 - F 2 + A y + B y = 0 (1)
УX = -F 2r + A x + B x = 0 (2)
UM yC = -P 1 * 32 + A y * 20 - B y * 10 = 0 (3)
UM yB = - P 1 * 42 + A y * 30 - F 2 * 10 = 0 (4)
UM xC = A x * 20 - V x * 10 = 0 (5)
UM xB = A x * 30 + F 2r * 10 = 0 (6)
Betrachten Sie die Gleichungen (3) und (4)
840 * 32 + A y * 20 - B y * 10 = 0
840 * 42 + A y * 30 - 507,5 *10 = 0
Aus der letzten Gleichung:
A y = 40355/30 = 1345 N
Aus der ersten Gleichung:
26880 + 26900 = 10*V y? V y = 20/10 = 2 N
Betrachten Sie die Gleichungen (5) und (6)
A x * 20 - B x * 10 = 0
A x * 30 + 203 * 10 = 0
Aus der letzten Gleichung A x = 2030/30 = 67,7 N
Aus der ersten Gleichung: 1353,3 = 10*V y? V y = 1353/10 = 135,3 N
Wir werden dies anhand der Gleichungen (1) und (2) überprüfen:
YY = -840 - 507,5 + 1345 + 2 = 0
УX = -203 + 67,7 + 135,3 = 0
Die Berechnungen wurden korrekt durchgeführt. Die Endreaktionen der Träger A und B sind:
A = = = 1346,7 N




B = = = 135,3 N