Понятие об ускорении. Движение с постоянным ускорением по прямой линии

План-конспект урока по теме «Скорость при прямолинейном движении с постоянным ускорением»

Дата :

Тема: «Скорость при прямолинейном движении с постоянным ускорением»

Цели:

Образовательная : Обеспечить и сформировать осознанное усвоение знаний о скорости при прямолинейном движении с постоянным ускорением;

Развивающая : Продолжить развитие навыков самостоятельной деятельности, навыков работы в группах.

Воспитательная : Формировать познавательный интерес к новым знаниям; воспитывать дисциплину поведения.

Тип урока: урок усвоения новых знаний

Оборудование и источники информации:

Исаченкова, Л. А. Физика: учеб. для 9 кл. учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, А. А. Сокольский; под ред. А. А. Сокольского. Минск: Народная асвета, 2015

Исаченкова, Л. А. Сборник задач по физике. 9 класс: пособие для учащихся учреждений общ. сред. образования с рус. яз. обучения / Л. А. Исаченкова, Г. В. Пальчик, В. В. Дорофейчик. Минск: Аверсэв, 2016, 2017.

Структура урока:

Организационный момент(5 мин)

Актуализация опорных знаний(5мин)

Изучение нового материала (15 мин)

Физкультминутка (2 мин)

Закрепление знаний (13мин)

Итоги урока(5 мин)

Организационный момент

Здравствуйте, садитесь! (Проверка присутствующих). Сегодня на уроке мы должны разобраться со скоростью при прямолинейном движении с постоянным ускорением. А это значит, что Тема урока : Скорость при прямолинейном движении с постоянным ускорением

Актуализация опорных знаний

Самое простое из всех неравномерных движении - прямолинейное движение с постоянным ускорением. Его называют равнопеременным.

Как изменяется скорость тела при равнопеременном движении?

Изучение нового материала

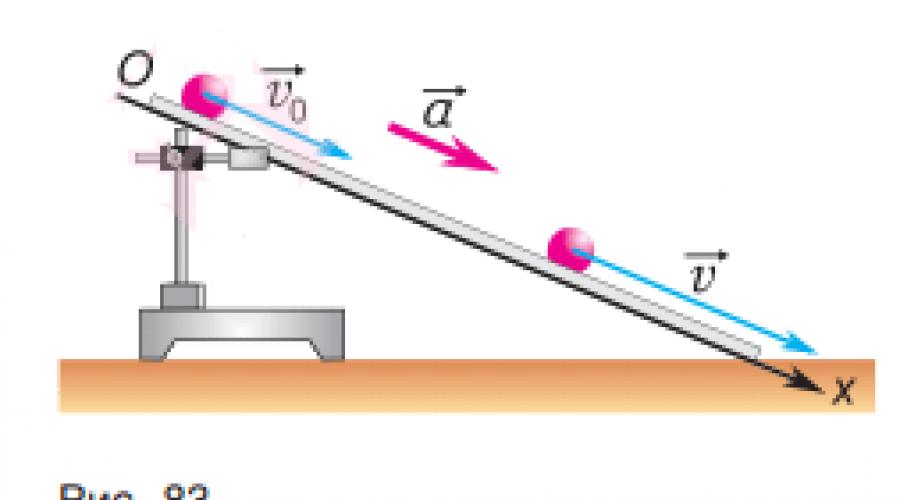
Рассмотрим движение стального шарика по наклонному желобу. Опыт показывает, что его ускорение практически постоянно:

Пусть в момент времени t = 0 шарик имел начальную скорость (рис. 83).

Как найти зависимость скорости шарика от времени?

Ускорение шарика а = . В нашем примере Δt = t , Δ - . Значит,

, откуда

При движении с постоянным ускорением скорость тела линейно зависит от времени.

Из равенств (1 ) и (2) следуют формулы для проекций:

Построим графики зависимости a x ( t ) и v x ( t ) (рис. 84, а, б).

Рис. 84

Согласно рисунку 83 а х = а > 0, = v 0 > 0.

Тогда зависимости a x ( t ) соответствует график 1 (см. рис. 84, а). Это прямая, параллельная оси времени. Зависимости v x ( t ) соответствует график , описывающий возрастание проекции ско рости (см. рис. 84, б). Понятно, что растет и модуль скорости. Шарик движется равноускоренно.

Рассмотрим второй пример (рис. 85). Теперь начальная скорость шарика направлена вдоль желоба вверх. Двигаясь вверх, шарик будет постепенно терять скорость. В точке А он на мгновение остановится и начнет скатываться вниз. Точку A называют точкой поворота.

Согласно рисунку 85 а х = - а < 0, = v 0 > 0, и формулам (3) и (4) соответствуют графики 2 и 2" (см. рис. 84, а , б).

График 2" показывает, что вначале, пока шарик двигался вверх, проекция скорости v x была положительна. Она уменьшалась и в момент времени t = стала равной нулю. В этот момент шарик достиг точки поворота A (см. рис. 85). В данной точке направление скорости шарика изменилось на противоположное и при t > проекция скорости стала отрицательной.

Из графика 2" (см. рис. 84, б) видно также, что до момента поворота модуль скорости уменьшался - шарик двигался вверх равнозамедленно. При t > t n модуль скорости растет - шарик движется вниз равноускоренно.

Постройте самостоятельно графики зависимости модуля скорости от времени для обоих примеров.

Какие еще закономерности равнопеременного движения необходимо знать?

В § 8 мы доказали, что для равномерного прямолинейного движения площадь фигуры между графиком v x и осью времени (см. рис. 57) численно равна проекции перемещения Δ r х . Можно доказать, что это правило применимо и для неравномерного движения. Тогда согласно рисунку 86 проекция перемещения Δ r х при равнопеременном движении определяется площадью трапеции ABCD . Эта площадь равна полусумме оснований трапеции умноженной на ее высоту AD .

В результате:

Так как среднее значение проекции скорости формулы (5)

следует:

При движении с постоянным ускорением соотношение (6) выполняется не только для проекции, но и для векторов скорости:

Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.

Формулы (5), (6) и (7) нельзя использовать для движения с непостоянным ускорением. Это может привести к грубым ошибкам.

Закрепление знаний

Разберем пример решения задачи со страницы 57:

Автомобиль двигался со скоростью, модуль которой = 72 . Увидев красный свет светофора, водитель на участке пути s = 50 м равномерно снизил скорость до = 18 . Определите характер движения автомобиля. Найдите направление и модуль ускорения, с которым двигался автомобиль при торможении.

Дано: Реше ние:

72 = 20 Движение автомобиля было равнозамедленным. Уско-

рение автомобиля направлено противоположно

18 = 5 скорости его движения.

Модуль ускорения:

s = 50 м

Время торможения:

а - ? Δ t =

Тогда

Ответ:

Итоги урока

При движении с постоянным ускорением скорость линейно зависит от времени.

При равноускоренном движении направления мгновенной скорости и ускорения совпадают, при равнозамедленном - они противоположны.

Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.

Организация домашнего задания

§ 12, упр. 7 № 1, 5

Рефлексия.

Продолжите фразы:

Сегодня на уроке я узнал…

Было интересно…

Знания, которые я получил на уроке, пригодятся

При равноускоренном движении справедливы следующие уравнения, которые мы приводим без вывода:

Как вы понимаете, векторная формула слева и две скалярные формулы справа равноправны. С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).

Зная, что  sx = x – xo  и   sy = y – yo  (см. § 12-е), из двух скалярных формул из правой верхней колонки получим уравнения для координат:

Поскольку ускорение при равноускоренном движении тела постоянно, то координатные оси всегда можно расположить так, чтобы вектор ускорения был направлен параллельно одной оси, например оси Y. Следовательно, уравнение движения вдоль оси X заметно упростится:

x  =  xo + υox t  + (0) и y  =  yo + υoy t  + ½ ay t²

Обратите внимание, что левое уравнение совпадает с уравнением равномерного прямолинейного движения (см. § 12-ж). Это означает, что равноускоренное движение может «складываться» из равномерного движения вдоль одной оси и равноускоренного движения вдоль другой. Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).

Задача . Вытянув руки, девочка подбросила шар. Он поднялся на 80 cм и вскоре упал к ногам девочки, пролетев 180 cм. С какой скоростью шар был подброшен и какую скорость шар имел при ударе о землю?

Возведём в квадрат обе части уравнения для проекции на ось Y мгновенной скорости: υy  =  υoy + ay t  (см. § 12-и). Получим равенство:

υy²  =  ( υoy + ay t )²  =  υoy² + 2 υoy ay t + ay² t²

Вынесем за скобки множитель  2 ay  только для двух правых слагаемых:

υy²  =  υoy² + 2 ay ( υoy t + ½ ay t² )

Заметим, что в скобках получилась формула для вычисления проекции перемещения:  sy = υoy t + ½ ay t². Заменяя её на sy , получим:

Решение. Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:

0 = υoy² + 2·(–g)·(+h) ⇒ υoy = ±√¯2gh = +4 м/с

Затем при начале движения из верхней точки вниз:

υy² = 0 + 2·(–g)·(–H) ⇒ υy = ±√¯2gh = –6 м/с

Ответ: шар был брошен вверх со скоростью 4 м/с, а в момент приземления имел скорость 6 м/с, направленную против оси Y.

Примечание. Надеемся, вы понимаете, что формула для квадрата проекции мгновенной скорости будет верна по аналогии и для оси X:

Если движение одномерное, то есть происходит только вдоль одной оси, можно пользоваться любой из двух формул в рамках.

§ 12-й. Движение с постоянным ускорением

При равноускоренном движении справедливы следующие уравнения, которые мы приводим без вывода:

Как вы понимаете, векторная формула слева и две скалярные формулы справа равноправны. С точки зрения алгебры, скалярные формулы означают, что при равноускоренном движении проекции перемещения зависят от времени по квадратичному закону. Сравните это с характером проекций мгновенной скорости (см. § 12-з).

Зная, что  s x  = x – x o  и   s y  = y – y o   (см. § 12-е), из двух скалярных формул из правой верхней колонки получим уравнения для координат:

Поскольку ускорение при равноускоренном движении тела постоянно, то координатные оси всегда можно расположить так, чтобы вектор ускорения был направлен параллельно одной оси, например оси Y. Следовательно, уравнение движения вдоль оси X заметно упростится:

x  =  x o + υ ox  t  + (0) и y  =  y o + υ oy  t  + ½ a y  t²

Обратите внимание, что левое уравнение совпадает с уравнением равномерного прямолинейного движения (см. § 12-ж). Это означает, что равноускоренное движение может «складываться» из равномерного движения вдоль одной оси и равноускоренного движения вдоль другой. Подтверждением этому служит опыт с ядром на яхте (см. § 12-б).

Задача . Вытянув руки, девочка подбросила шар. Он поднялся на 80 cм и вскоре упал к ногам девочки, пролетев 180 cм. С какой скоростью шар был подброшен и какую скорость шар имел при ударе о землю?

Возведём в квадрат обе части уравнения для проекции на ось Y мгновенной скорости: υ y  =  υ oy + a y  t  (см. § 12-и). Получим равенство:

υ y ²  =  ( υ oy + a y  t )²  =  υ oy ² + 2 υ oy  a y  t + a y ² t²

Вынесем за скобки множитель  2 a y   только для двух правых слагаемых:

υ y ²  =  υ oy ² + 2 a y  ( υ oy  t + ½ a y  t² )

Заметим, что в скобках получилась формула для вычисления проекции перемещения:  s y = υ oy  t + ½ a y  t². Заменяя её на s y , получим:

Решение. Сделаем чертёж: ось Y направим вверх, а начало координат поместим на земле у ног девочки. Применим выведенную нами формулу для квадрата проекции скорости сначала в верхней точке подъёма шара:

0 = υ oy ² + 2·(–g)·(+h) ⇒ υ oy = ±√¯2gh = +4 м/с

Затем при начале движения из верхней точки вниз:

υ y ² = 0 + 2·(–g)·(–H) ⇒ υ y = ±√¯2gh = –6 м/с

Ответ: шар был брошен вверх со скоростью 4 м/с, а в момент приземления имел скорость 6 м/с, направленную против оси Y.

Примечание. Надеемся, вы понимаете, что формула для квадрата проекции мгновенной скорости будет верна по аналогии и для оси X.

Движение с постоянным ускорением–это такое движение, при котором вектор ускорения остается постоянным как по величине, так и по направлению. Примером такого типа движения может служить движения точки в поле силы тяжести (как вертикально, так и под углом к горизонту).

Используя определение ускорения получим следующее соотношение

После интегрирования имеем равенство
.

С учетом того, что вектор мгновенной скорости есть
, будем иметь следующее выражение

Интегрирование последнего выражение дает следующее соотношение

. Откуда имеем получаем уравнение движения точки с постоянным ускорением

.

Примеры векторных уравнений движения материальной точки

Равномерное прямолинейное движение (
):

. (1.7)

Движение с постоянным ускорением (
):

. (1.8)

Зависимость скорости от времени при движении точки с постоянным ускорением имеет вид:

. (1.9)

Вопросы для самоконтроля.

Сформулируйте определение механического движения.

Дайте определение материальной точки.

Каким образом определяется положение материальной точки в пространстве в векторном способе описания движения?

В чем сущность векторного метода описания механического движения? Какие характеристики используются для описания этого движения?

Дайте определения векторов средней и мгновенной скорости. Как определяется направление этих векторов?

Дайте определение векторов среднего и мгновенного ускорений.

Какое из соотношений является уравнением движения точки с постоянным ускорением? Какое соотношение определяет зависимость вектора скорости от времени?

§1.2. Координатный способ описания движения

В координатном способе для описания движения выбирают систему координат (например, декартову). Начало отсчета жестко закрепляют с выбранным телом (телом отсчета ). Пусть
единичные орты, направленные в положительные стороны осейOX, OY и OZ соответственно. Положение точки задается координатами
.

Вектор мгновенной скорости определяется следующим образом:

где
проекции вектора скорости на оси координат, а
производные от координат по времени.

Длина вектора скорости связана с его проекциями соотношением:

. (1.11)

Для вектора мгновенного ускорения справедливо соотношение:

где
проекции вектора ускорения на оси координат, а
производные по времени от проекций вектора скорости.

Длина вектора мгновенного ускорения находится по формуле:

. (1.13)

Примеры уравнений движения точки в декартовой системе координат

. (1.14)

Уравнения движения:
. (1.15)

Зависимости проекций вектора скорости на оси координат от времени:

(1.16)

Вопросы для самоконтроля.

В чем сущность координатного способа описания движения?

Каким соотношением определяется вектор мгновенной скорости? По какой формуле вычисляется величина вектора скорости?

Каким соотношением определяется вектор мгновенного ускорения? По какой формуле вычисляется величина вектора мгновенного ускорения?

Какие соотношения называют уравнениями равномерного движения точки?

Какие соотношения называют уравнениями движения с постоянным ускорением? По каким формулам рассчитывают проекции мгновенной скорости точки на оси координат?

Положение тел относительно выбранной системы координат принято характеризовать радиусом-вектором , зависящим от времени. Тогда положение тела в пространстве в любой момент времени можно найти по формуле:

.

(Напомним, что в этом и заключается основная задача механики.)

Среди множества различных видов движения самым простым является равномерное – движение с постоянной скоростью (нулевым ускорением), причем неизменным должен оставаться вектор скорости (). Очевидно, что такое движение может быть только прямолинейным. Именно при равномерном движении перемещение вычисляется по формуле:

Иногда тело движется по криволинейной траектории так, что модуль скорости остается постоянным () (такое движение нельзя назвать равномерным и к нему нельзя применить формулу). В этом случае пройденный путь может быть вычислен по простой формуле:

Примером такого движения является движение по окружности с постоянной по модулю скоростью .

Более сложным является равноускоренное движение – движение с постоянным ускорением (). Для такого движения справедливы две формулы кинематики:

из которых можно получить две дополнительные формулы, которые часто могут быть полезны при решении задач:

;

Равноускоренное движение не обязательно должно быть прямолинейным. Необходимо лишь, чтобы вектор ускорения оставался постоянным. Примером равноускоренного, но не всегда прямолинейного движения, является движение с ускорением свободного падения (g = 9,81 м/с 2), направленным вертикально вниз.

Из школьного курса физики знакомо и более сложное движение – гармонические колебания маятника, для которого формулы – не справедливы.

При движении тела по окружности с постоянной по модулю скоростью оно движется с так называемым нормальным (центростремительным ) ускорением

направленным к центру окружности и перпендикулярным скорости движения.

В более общем случае движения по криволинейной траектории с меняющейся скоростью ускорение тела можно разложить на две взаимно перпендикулярные составляющие и представить в виде суммы тангенциального (касательного) и нормального (перпендикулярного, центростремительного) ускорения:

,

где – орт вектора скорости и орт нормали к траектории; R – радиус кривизны траектории.

Движение тел всегда описывается относительно какой-либо системы отсчета (СО). При решении задач необходимо выбрать наиболее удобную СО. Для поступательно движущихся СО формула

позволяет легко переходить от одной СО к другой. В формуле – скорость тела относительно одной СО; – скорость тела относительно второй СО; – скорость второй СО относительно первой.

Вопросы для самопроверки и задачи

1) Модель материальной точки: в чем ее суть и смысл?

2) Сформулируйте определение равномерного, равноускоренного движения.

3) Сформулируйте определения основных кинематических величин (радиуса-вектора, перемещения, скорости, ускорения, тангенциального и нормального ускорения).

4) Напишите формулы кинематики равноускоренного движения, выведите их.

5) Сформулируйте принцип относительности Галилея.

2.1.1. Прямолинейное движение

Задача 22. (1) Автомобиль движется по прямолинейному участку дороги с постоянной скоростью 90 . Найти перемещение автомобиля за 3,3 мин и его положение в этот же момент времени, если в начальный момент времени автомобиль находился в точке, координата которой равна 12,23 км, а ось Ox направлена 1) вдоль движения автомобиля; 2) против движения автомобиля.

Задача 23. (1) Велосипедист движется по загородной дороге на север со скоростью 12 в течение 8,5 мин, затем он, свернув направо на перекрестке, проехал еще 4,5 км. Найти перемещение велосипедиста за время его движения.

Задача 24. (1) Конькобежец движется прямолинейно с ускорением 2,6 , и за 5,3 с его скорость увеличилась до 18 . Найти начальное значение скорости конькобежца. Какое расстояние пробежит спортсмен за это время?

Задача 25. (1) Автомобиль движется прямолинейно, притормаживая перед знаком ограничения скорости 40 с ускорением 2,3 Сколько времени длилось такое движение, если перед началом торможения скорость автомобиля была равна 70 ? На каком расстоянии от знака водитель начал тормозить?

Задача 26. (1) С каким ускорением движется поезд, если на пути 1200 м его скорость возросла от 10 до 20 ? Сколько времени затратил поезд на этот путь?

Задача 27. (1) Тело, брошенное вертикально вверх, вернулось на землю через 3 с. Какова была начальная скорость тела? На какой максимальной высоте оно побывало?

Задача 28. (2) Тело на веревке поднимают с поверхности земли с ускорением 2,7 м/с 2 вертикально вверх из состояния покоя. Через 5,8 с веревка оборвалась. Сколько времени двигалось тело до земли после того, как оборвалась веревка? Сопротивлением воздуха пренебречь.

Задача 29. (2) Тело начинает двигаться без начальной скорости с ускорением 2,4 Определить путь, пройденный телом за первые 16 с от начала движения, и путь, пройденный за последующие 16 с. С какой средней скоростью двигалось тело эти 32 с?

2.1.2. Равноускоренное движение в плоскости

Задача 30. (1) Баскетболист бросает мяч в кольцо со скоростью 8,5 под углом 63 о к горизонту. С какой скоростью мяч попал в кольцо, если долетел до него за 0,93 с?

Задача 31. (1) Баскетболист бросает мяч в кольцо. В момент броска мяч находится на высоте 2,05 м, а через 0,88 с падает в кольцо, расположенное на высоте 3,05 м. С какого расстояния от кольца (по горизонтали) произведен бросок, если мяч был брошен под углом 56 о к горизонту?

Задача 32. (2) Мяч брошен горизонтально со скоростью 13 , спустя некоторое время его скорость оказалась равной 18 . Найти перемещение мяча за это время. Сопротивлением воздуха пренебречь.

Задача 33. (2) Тело брошено под некоторым углом к горизонту с начальной скоростью 17 м/с. Найти величину этого угла, если дальность полета тела в 4,3 раза больше максимальной высоты подъема.

Задача 34. (2) Бомбардировщик, пикирующий со скоростью 360 км/ч, сбрасывает бомбу с высоты 430 м, находясь по горизонтали на расстоянии 250 м от цели. Под каким углом должен пикировать бомбардировщик? На какой высоте окажется бомба спустя 2 с от начала падения? Какую скорость она будет иметь в этой точке?

Задача 35. (2) Самолет, летевший на высоте 2940 м со скоростью 410 км/ч, сбросил бомбу. За какое время до прохождения над целью и на каком расстоянии от нее самолет должен сбросить бомбу, чтобы попасть в цель? Найти модуль и направление скорости бомбы спустя 8,5 с от начала ее падения. Сопротивлением воздуха пренебречь.

Задача 36. (2) Снаряд, выпущенный под углом 36,6 о к горизонту, дважды был на одной и той же высоте: спустя 13 и 66 с после вылета. Определить начальную скорость, максимальную высоту подъема и дальность полета снаряда. Сопротивлением воздуха пренебречь.

2.1.3. Движение по окружности

Задача 37. (2) Грузило, движущееся на леске по окружности с постоянным тангенциальным ускорением, к концу восьмого оборота имело скорость 6,4 м/с, а после 30 с движения его нормальное ускорение стало 92 м/с 2 . Найти радиус этой окружности.

Задача 38. (2) Мальчик, катающийся на карусели, движется при остановке карусели по окружности радиусом 9,5 м и проходит путь 8,8 м, имея в начале этой дуги скорость 3,6 м/с, а в конце – 1,4 м/с. Определить полное ускорение мальчика в начале и конце дуги, а также время его движения по этой дуге.

Задача 39. (2) Муха, сидящая на краю лопасти вентилятора, при его включении движется по окружности радиусом 32 см с постоянным тангенциальным ускорением 4,6 см/с 2 . Через сколько времени после начала движения нормальное ускорение будет вдвое больше тангенциального и чему будет равна линейная скорость мухи в этот момент времени? Сколько оборотов муха сделает за это время?

Задача 40. (2) При открывании двери ручка из состояния покоя движется по окружности радиусом 68 см с постоянным тангенциальным ускорением, равным 0,32 м/с 2 . Найти зависимость полного ускорения ручки от времени.

Задача 41. (3) Для экономии места въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиусом 65 м. Полотно дороги составляет с горизонтальной плоскостью угол 4,8 о. Найти ускорение автомобиля, движущегося по этой дороге с постоянной по модулю скоростью, равной 85 км/ч?

2.1.4. Относительность движения

Задача 42. (2) Два корабля движутся относительно берегов со скоростью 9,00 и 12,0 узлов (1 узел = 0,514 м/с), направленной под углом 30 и 60 о к меридиану соответственно. С какой скоростью второй корабль движется относительно первого?

Задача 43. (3) Мальчик, который может плавать со скоростью, в 2,5 раза меньшей скорости течения реки, хочет переплыть эту реку так, чтобы его как можно меньше снесло вниз по течению. Под каким углом к берегу мальчик должен плыть? На какое расстояние его снесет, если ширина реки равна 190 м.

Задача 44. (3) Два тела одновременно начинают двигаться из одной точки в поле силы тяжести с одинаковой скоростью, равной 2,6 м/с. Скорость одного тела направлена под углом π/4, а другого – под углом –π/4 к горизонту. Определить относительную скорость этих тел через 2,9 с после начала их движения.